
Nouveauté 20/09/2005 : participez à la traduction de cette page en anglais : Solitaire_english.html

Nouveauté 20/09/2005 : participez à la traduction de cette page en anglais : Solitaire_english.html
Contactez moi à eternitygames@free.fr si vous souhaitez participer (en traduisant juste quelques lignes, vous accélérerez considérablement la traduction de cette page, encore merci)


Il existe deux types de solitaire principalement, le solitaire français et le solitaire anglais :
Je me suis intéressé principalement au solitaire anglais car c'est le solitaire le plus connu mais les nombreuses variantes triangulaires, carrées et autres sont toutes aussi intéressantes bien sûr.
| Historique du jeu : |
| Origine du Solitaire : |
Le solitaire serait un jeu romain : Ovide l'aurait décrit en grand détail.
Pourtant, il n'aurait été connu en France qu'au XVIème siècle, et par une voie toute différente. Un Français qui explorait alors l'Amérique remarqua la façon dont les Indiens plantaient leurs flèches dans les trous d'une planchette creusée symétriquement. Il inventa les règles de ce jeu.
Source : http://deesse.univ-lemans.fr/~marson/sol1/sol/historique.htmlLa légende veut que le solitaire fut inventé par un prisonnier d'origine noble emprisonné à la Bastille pendant la seconde moitié du XVIIème siècle. La première trace écrite en France datte de 1710 et est due à Leibniz qui s'est intéressé de très près à ce jeu : Il sert, dit-il, à perfectionner l'art de méditer. Mais comme il en existe de plusieurs types, toutes les origines sont possibles...
| Princesse de Soubise : |
La princesse de Soubise (Anne Chabot de Rohan 1663-1709) se fit peindre avec un
solitaire à la main par Claude-Auguste Berey :

Et cette gravure éditée par Antoine Trouvain à la fin du XVIIème siècle :
Bibliothèque nationale de France (Paris)

Vous notez le titre : Dame de qualité jouant au solitaire qui nous fait sourire aujourd'hui et même à l'époque j'imagine.
Le solitaire obtint son plus grand succès au XVIIIème siècle.
Différentes versions du Solitaire commercialisées à toutes époques
sont disponibles à cette adresse :
http://www.ahs.uwaterloo.ca/~museum/puzzles/solitare/
Leibniz, qui en fut grand amateur, a longuement épilogué sur son intérêt.
Il sert, dit-il, à perfectionner l'art de méditer.
| Livre de John H. Conway : |
Le texte suivant est traduit du livre
E.R.Berlekamp,J.H.Conway,R.K.Guy,Winning Ways for your Mathematical Plays, 1982, volume 2, chapitre 23, ISBN 01-12-091102-7

| Leibnitz et le Solitaire inversé : |
Le jeu appelé Solitaire me plait beaucoup. J'y joue dans l'ordre inverse. C'est à dire qu'à la place de suivre les règles du jeu, qui sont de sauter sur une place vide et d'enlever la pièce qui a été sautée, je pensais que c'était mieux de reconstruire ce qui a été démolit, en remplissant un trou vide quand on a sauté par-dessus.
Leibnitz

La philosophie de Leibnitz :
Le solitaire à l'envers est comme le solitaire à l'endroit avec les notions vide et remplit inter changées.
Le célèbre philosophe pensait pleinement que jouer au solitaire
à l'envers était différent d'y jouer à l'endroit, mais en fait
c'est réellement exactement pareil !
Pour le prouver regardons ce qui arrive quand il fait un mouvement
à l'envers.
Leibnitz voit ça en prenant la pièce t qui saute
dans le trou r puis en remplissant le trou vide s.
Mais la figure dessus montre qu'on peut voir ça comme le trou r
sautant par-dessus le trou s pour arriver sur la pièce t
qui devient un trou à son tour. Bien-sûr on enlève le trou sauté,
ce qui revient à insérer une pièce dans cette logique !!!
Comme tous les grands mathématiciens, il avait l'esprit un peu tordu mais en fait le solitaire inversé revient au même que la Solitaire classique à l'endroit.
| Études théoriques sur le Solitaire : |
John H. Conway et John D. Beasley ont fait les deux ouvrages
références en matière de Solitaire.
Un des problèmes importants du Solitaire est sa faisabilité, c'est à
dire savoir si une configuration de départ peut aboutir
à une configuration d'arrivée : l'existence de solutions donc.
La première étude théorique sérieuse du jeu (après Leibnitz)
a apparemment été faite par Suremain de Missery en 1841-1842.
Cette étude a été reportée par J.N Vallot, sinon elle aurait été sûrement perdue :
Rapport sur un travail de Suremain de Missery : Théorie générale du jeu de Solitaire,
considéré comme problème d'analyse et de situation. Compte-rendu
des travaux de l'Académie de Sciences, Arts et Belles-lettres de Dijon (1841-1842) page 58-70.
La règle de trois de Suremain de Missery est d'une ingéniosité remarquable !
(cf. ici pour les détails de cette règle).
Je n'ai hélas pas lu le compte-rendu de Vallot : je ne connais donc
pas l'idée intuitive qui a permis à Suremain de Missery d'atteindre ce résultat.
En effet, la démonstration mathématique rigoureuse
de La règle de trois présentée ici n'explique pas comment
Suremain de Missery a eu cette idée (bien au contraire).
Après Suremain de Missery, le Solitaire est ensuite tombé dans l'oubli du
point de vue théorique jusque dans les années 60 où Conway et Boardman
(université de Cambridge) s'y sont ré intéressés.
Le groupe de l'université de Cambridge mené par Conway
a étudié à nouveau le problème de faisabilité du Solitaire
et a aboutit à de nouvelles conditions de faisabilité
avec le le cône du Solitaire, inéquations sur le cône connues sous
les noms de Fonctions en Pagode 1961 (cf. Fonctions en Pagode (problème de l'armée infinie de pions)).
Une nouvelle condition de faisabilité a été découverte assez récemment par David Avis, Antoine Deza et Shmuel Onn qui généralisent La règle de trois : le Lattice criterion.
Je vous invite d'ailleurs à lire leurs publications sur le Solitaire :
Tous les fichiers sont au format PostScript, il vous faudra donc installer Ghostscript
puis GSview pour les visualiser et imprimer :
http://www.cs.wisc.edu/~ghost/doc/AFPL/get650.htm
A Combinatorial Approach to the Solitaire Game est aussi au format PDF,
il vous faudra donc Acrobat Reader version 4 minimum puisque
ce fichier me posait quelques problèmes avec la version 3 :
![]()
Ces publications sont vraiment intéressantes si vous connaissez un peu l'algèbre linéaire.
| But du Solitaire : |
Je ne crois pas utile de rappeler les règles du Solitaire que
vous connaissez, la seule règle à retenir étant qu'un pion peut
sauter par-dessus un pion voisin horizontalement ou verticalement
(pas en diagonal sauf sur certaines versions du Solitaire moins connues) :
Le pion sauté étant alors à enlever bien sûr.
Le but ou le challenge principal du Solitaire est d'atteindre l'inverse de la position de départ (même si au Solitaire français c'est impossible).
Le cas le plus intéressant est celui où l'on débute avec un plateau remplit sauf le pion du milieu (qui est enlevé) et dont le but est alors d'atteindre le plateau opposé ou inverse : c'est à dire un plateau vide sauf le pion du milieu qui doit rester seul.
C'est d'ailleurs ce dernier cas classique des classiques qui est
considéré comme le jeu du Solitaire lui-même mais vous pouvez vous inventer
autant de configurations de départ et d'arrivée que vous souhaitez bien sûr.
Certaines des configurations d'ailleurs portent des noms :
http://deesse.univ-lemans.fr/~marson/sol1/sol/figures.html
| Critères de non faisabilité du Solitaire : |
Les problèmes de faisabilité du Solitaire sont de déterminer si un couple de configuration de plateau (P,P') est faisable, c'est à dire s'il existe une séquence de coups valides transformant P en P'.
Des conditions nécessaires de faisabilité du Solitaire sont nombreuses (même presque infinies
avec les fonctions en Pagode) mais des conditions nécessaires et suffisantes restent à découvrir.
La complexité du problème de faisabilité sur un plateau n x n est NP-complet d'après Uehara et Iwata
donc de telles conditions nécessaires et suffisantes sont improbables d'exister.
R. Uehara R. et S. Iwata : Generalized Hi-Q is NP-complete. Trans. IEICE E 73 (1990) Pages 270-273.
Voici une présentation de ces critères de non faisabilité :
Les démonstrations données par David Avis, Antoine Deza et Shmuel Onn sur la La règle de trois comme pour le Cône du Solitaire ou le Lattice criterion (critère étendu de la règle de trois) sont extrêmement intéressantes, c'est pourquoi je les résume ici en utilisant leurs terminologies mais lisez leurs publications pour avoir des démonstrations rigoureuses.
Un plateau du Solitaire est considéré par analogie à la géométrie à un point à n dimensions (33 pour le solitaire anglais) ou un tableau à 33 cases sur une rangée si vous préférez. Chaque composante du point (ou case du tableau) prend la valeur 0 si il y a 0 pion, la valeur 1 si il y a 1 pion et on autorise une extension en permettant aussi les valeurs supérieures à 1 et même les valeurs négatives : les entiers relatifs donc. Il peut donc y avoir 2 pions dans une case et même -1 pion !
Un mouvement (coup ou saut si vous préférez) est alors un vecteur à n dimensions, ce qui permet d'additionner Plateaux et mouvements (en géométrie, un vecteur est la différence de 2 points).
Comme pour les points du plan où le point P additionné au vecteur M est le point P'
Pour qu'un mouvement soit valide, il faut que M présente deux composantes à -1 et une composante à 1 :
Mais vous verrez qu'on pourra autoriser des mouvements non valides pour démontrer la
non faisabilité de couples de configurations (P,P') avec les fonctions en Pagode (Fonctions en Pagode et Cône du Solitaire).
Vous voyez aussi déjà pourquoi on autorise les nombres négatif avec -1.
Soit S l'ensemble des coordonnées (i,j) représentant les emplacements des trous/pions du Solitaire, on a au Solitaire anglais :
![]()
Une configuration du Solitaire valide ou non est donc un vecteur de ZS (Z étant les entiers relatifs).
Une configuration du Solitaire valide est un vecteur de BS (B = {0,1}).
Le complémentaire P d'une configuration valide ![]() {0,1}S
{0,1}S
où ![]() RS
RS
Définition de la faisabilité :
Si (P,P') est le couple de configurations (départ, arrivée) alors
(P,P') est faisable à condition qu'il existe k mouvements valides allant de P à P' : M1,...,Mk
vérifiant ces deux relations :

Un plateau valide étant un plateau avec 0 ou 1 pion dans chaque trou, une configuration du Solitaire donc.
Le Solitaire anglais admet 76 mouvements valides différents donc les k mouvements Mi en font nécessairement partie dans le cas du Solitaire anglais (k est le nombre de mouvements nécessaire pour aller de P à P', c'est à dire le nombre de pions de P' moins le nombre de pions de P).
| La règle de trois : |
La règle de trois détermine l'impossibilité de certains problèmes en étendant la règle de base du jeu.
On utilise une relation d'équivalence étendant la règle de base du jeu (liant 2 configurations P et P'), et on démontre que si P n'est pas en relation avec P' (P non équivalent à P') alors le couple de configurations (P,P') n'est pas faisable au sens de la définition de la faisabilité.
On s'intéresse pour cela à l'expression suivante :

Les Mi sont ici les m mouvements valides du jeu (76 mouvements valides m au solitaire anglais, k < m)
Cette dernière expression est vraie (possède des solutions) en particulier si les 2 conditions de la définition de la faisabilité sont vérifiées :

Les Mi dans la définition de la faisabilité sont les k mouvements valides transformant P en P'.
Démonstration :


La faisabilité est donc en quelque sorte un cas particulier (ou sous-ensemble) de l'ensemble des solutions engendrées par l'expression :

L'expression est nécessairement vraie (possède des solutions) si la faisabilité est prouvée (faisabilité implique expression vraie).
L'expression est plus étendue, plus large ou moins contraignante que la définition de la faisabilité. Si elle est vraie, elle n'implique pas la faisabilité mais si elle est fausse elle implique la non - faisabilité du couple (P,P'), car dans ce cas, le couple (P,P') ne peut plus être décomposé en mouvements valides (combinaisons linéaires de mouvements valides).
On a donc la propriété :

Définition :
On dit que P est en relation avec P' si il existe une combinaison linéaire de mouvements M (valides) transformant P en P' :

La combinaison linéaire de mouvements Mi est sans contrainte et autorise donc les mouvements négatifs et les multi mouvements identiques et superposés.
Ce qui revient alors à autoriser que tous les plateaux intermédiaires issus des k mouvements aient un nombre de pions quelconque, même négatif :

On dit alors que : P est équivalent à P' car c'est une relation d'équivalence (relation réflexive, symétrique et transitive) :
1) relation réflexive :
Si P' = P
P' - P = 0

Vérifié quel que soit P avec ai = 0 (i = 1,...,m)
Donc P est en relation avec P quel que soit P (réflexivité)
2) relation symétrique :
P est en relation avec P' implique :

Et donc P est en relation avec P' implique P' est en relation avec P quel que soient P et P' (symétrie)
3) relation transitive :
P est en relation avec P' et P' est en relation avec P'' impliquent :



Et donc P est en relation avec P' et P' est en relation avec P'' impliquent P est en relation avec P'' quels que soient P, P' et P'' (transitivité)
On a alors la propriété suivante :

Réduisons une configuration de solitaire en utilisant les règles suivantes d'équivalence sur tous les triplets du jeu (horizontaux ou verticaux) :
D'où :
Par addition :
Exemple :
Étendons le triplet (0,2,0) :
D'où :
Nous avons les 5 règles élémentaires suivantes :
(2) + (5) implique (-1,1,1) + (2,0,0) = (1,1,1) équivalent à (0,0,0) qui est la propriété la plus représentative de la règle de 3.
Le chapitre 2 du document suivant de Bernard BARNEOUD illustre très bien graphiquement ces équivalences : Bernard BARNEOUD - Solitaire-v2.pdf
Ces règles peuvent s'écrirent également sur un triplet (a,b,c) :
Ou encore :
Exemple : a+ b + c = 0, a + c = b
Appliquons ces règles sur tous les triplets du jeu :
Le livre de Edouard LUCAS "Récréations mathématiques Tome 1 (2nde édition) 1891" à partir de la page 118 (Le jeu du Solitaire - cinquième récréation) explique la règle de trois en utilisant un langage imagé (si vous comprenez mieux par une explication verbale que par un joli graphique, vous apprécierez) : vous pouvez le télécharger sur le site Gallica de la Bibliothèque Nationale de France http://gallica.bnf.fr qui le propose en libre téléchargement (à usage privé) : E. LUCAS - Récréations mathématiques -Tome 1 (2nde édition). J'en fais une copie (format PDF) sur ce site par sécurité (et à mon usage privé) : E. LUCAS - Le Solitaire.pdf mais je vous invite à le télécharger sur le site Gallica de la Bibliothèque Nationale de France qui elle seule possède les droits d'auteur (et de diffusion) de ce livre. Vous pouvez retrouver la liste des publications de Edouard LUCAS sur ce site : http://edouardlucas.free.fr/gb/publi.html (voir la publication n°148 pour le livre Récréations mathématiques Tome 1).
La règle de trois a, d'après le livre d'Edouard LUCAS, été imaginée par REISS et perfectionnée par HERMARY (voir page 118 et 119 pour les références).
Tous les pions peuvent être regroupés un à un au centre d'un carré de 3 x 3 = 9 cases en remarquant par exemple que (1,0,0) est équivalent à (0,1,1) qui est équivalent à (0,0,0,1) soit un décalage de 3 cases (vers la droite dans ce cas), ce qui permet d'atteindre de proche en proche le carré 3 x 3 au centre du jeu (voir page 122 du livre de E. LUCAS).
Une fois le carré de 3 x 3 cases établi, on peut le réduire en un carré de 2 x 2 en utilisant les remarques suivantes (voir page 124 et 125 du livre de E. LUCAS) :
| colonne a | colonne b | colonne c | |
| a2 | b2 | c2 | ligne 2 |
| a1 | b1 | c1 | ligne 1 |
| a0 | b0 | c0 | ligne 0 |
devient par addition de haut en bas :
| colonne a | colonne b | colonne c | |
| 0 | 0 | 0 | ligne 2 |
| a1+a2 | b1+b2 | c1+c2 | ligne 1 |
| a0+a2 | b0+b2 | c0+c2 | ligne 0 |
devient par addition de droite à gauche :
| colonne a | colonne b | colonne c | |
| 0 | 0 | 0 | ligne 2 |
| a1+a2+c1+c2 | b1+b2+c1+c2 | 0 | ligne 1 |
| a0+a2+c0+c2 | b0+b2+c0+c2 | 0 | ligne 0 |
Nous voici avec un carré de 2 x 2 que nous pouvons réduire à un carré 2 x 2 rempli de 1 et de 0 en continuant d'appliquer les règles précédentes :
Il y a donc 16 configurations possibles de carrés 2 x 2 : {(0,0,0,0),(0,0,0,1),{0,0,1,0),(0,1,0,0),(1,0,0,0),(0,0,1,1),(0,1,0,1),(0,1,1,0),(1,0,0,1),(1,0,1,0),(1,1,0,0),(1,1,0,1),(1,1,1,0),(1,1,1,1) répartis en 3 classes (voir page 127 du livre de E. LUCAS) :
Nous en venons à la propriété importante de la règle de trois :
(P,P') est faisable si les positions réduites (carrés de 4 cases remplis de 0 et de 1) issues des positions de départ P et d'arrivée P' sont identiques.
(si les positions réduites sont identiques, on ne peut rien conclure sur la faisabilité, par contre si elles sont différentes, on en conclu que (P,P') n'est pas faisable)
Démonstration :
Notons F(P) la position réduite de P : carré de 4 cases remplies de 1 et de 0
La propriété à démontrer s'écrit :
(P,P') faisable ==> P est équivalent à P' ==> F(P) équivalent à F(P') ==> F(P) = F(P')
1) Démonstration de (P,P') faisable ==> P est équivalent à P' :
Cette propriété a déjà été démontrée ici :

2) Démonstration de P équivalent à P' ==> F(P) équivalent à F(P') :
P est équivalent à F(P) si :

On a vu justement que F(P) est la réduction de P par l'application d'une combinaison linéaire de mouvements Mi valides suivant le procédé de réduction décrit précédemment.
Donc P est équivalent à F(P) (propriété vraie pour tout P si F(P) existe)
Par symétrie, F(P) est équivalent à P
De même, P' est équivalent à F(P')
Par transitivité : F(P) équivalent à P et P équivalent à P' et P' équivalent à F(P') ==> F(P) équivalent à F(P')
F(P) équivalent à P est toujours vrai, P' équivalent à F(P') est toujours vrai, donc F(P) équivalent à P et P' équivalent à F(P') est toujours vrai
Et donc : P équivalent à P' ==> F(P) équivalent à F(P') (F(P) équivalent à P équivalent à P' équivalent à F(P') ==> F(P) équivalent à F(P') )
De même par transitivité : P équivalent à F(P) et F(P) équivalent à F(P') et F(P') équivalent à P' ==> P équivalent à P'
P équivalent à F(P) est toujours vrai, F(P') équivalent à P' est toujours vrai, donc P équivalent à F(P) et F(P') équivalent à P' est toujours vrai
Et donc : F(P) équivalent à F(P)' ==> P équivalent à P' ( P équivalent à F(P) équivalent à F(P') équivalent à P' ==> P équivalent à P' )
On a donc : P équivalent à P' <==> F(P) équivalent à F(P')
3) Démonstration de F(P) est équivalent à F(P') ==>F(P) = F(P') :
Il y a bien qu'une seule forme réduite F(P) pour tout F(P) équivalent à F(P')
Démontrons cette unicité de la position réduite F(P) pour tout F(P) équivalent à F(P') :
Soit :


Il y a m=12 mouvements Mi valides dans un carré 3 x 3 (de 9 cases) :







Soient L1,..,L9, les 9 lignes du système linéaire :

Appliquons les combinaisons linéaires suivantes sur les lignes du système :



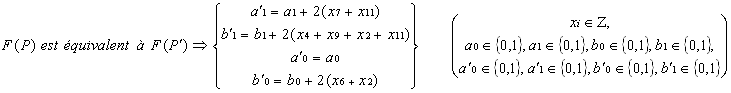

Donc a1 et a'1 ont la même parité, b1 et b'1 ont la même parité, a0 et a'0 sont égaux et b0 et b'0 ont la même parité.




L'unicité est ainsi démontrée.
Démonstration similaire en calculant les solutions du système (rappel d'algèbre linéaire)
On a donc bien : F(P) est équivalent à F(P') ==> F(P) = F(P')
Plus simplement, dans livre de E. LUCAS pages 125 et 126, il est démontré l'unicité de la position réduite F(P) pour tout F(P) équivalent à F(P'), en remarquant que les nombres dans les 4 cases du carré de la position réduite, garde la même parité quelque soit le nombre de coups joués en supplément, dans le carré 3x3 (ce qui revient au même que la démonstration précédente).
Remarquons que F(P) = F(P') ==> F(P) est équivalent à F(P) et F(P) = F(P') ==> F(P) est équivalent à F(P') (car F(P) est équivalent à F(P) est toujours vrai : réflexivité)
Et donc : F(P) = F(P') ==> F(P) est équivalent à F(P')
On a donc : F(P) est équivalent à F(P') <==> F(P) = F(P')
De 1), 2) et 3), on en déduit que :
(P,P') faisable ==> P est équivalent à P' <==> F(P) équivalent à F(P') <==> F(P) = F(P')
Donc (P,P') faisable ==> F(P) = F(P')
La propriété est ainsi démontrée :
(P,P') est faisable si les positions réduites (carrés de 4 cases remplis de 0 et de 1) issues des positions de départ P et d'arrivée P' sont identiques.
(si les positions réduites F(P) et F(P') sont identiques, on ne peut rien conclure sur la faisabilité, par contre si elles sont différentes, on en conclu que (P,P') n'est pas faisable)
La règle de trois avec la théorie des groupes (voir aussi pour une 1ère approche : http://www.cut-the-knot.com/proofs/PegsAndGroups.shtml) :
Soit G un ensemble de 4 éléments {a,b,c,e} vérifiant cette table d'addition :
Cet ensemble G est donc un Groupe commutatif (dit abélien), avec e comme élément neutre (voir la table d'addition "Cayley table" sur http://www.cut-the-knot.com/proofs/PegsAndGroups.shtml).
Soient g1, g2 : ZS ![]() G
G
g1(i,j) et g2(i,j) sont deux fonctions qui associent aux coordonnées (i,j) d'une case du Solitaire un élément de G
telles que :

Cette figure représente g1(i,j) et g2(i,j) au Solitaire anglais :

Par exemple :
| g1(0,0)=a, | g2(0,0)=a |
| g1(-1,-3)=c, | g2(-1,-3)=c |
| g1(1,3)=b, | g2(1,3)=b |
| g1(3,1)=b, | g2(3,1)=c |
| g1(3,-1)=c, | g2(3,-1)=b |
| g1(1,-3)=b, | g2(1,-3)=b |
| g1(-1,-3)=c, | g2(-1,-3)=c |
| g1(-3,-1)=c, | g2(-3,-1)=b |
| g1(-3,-1)=b, | g2(-3,-1)=c |
Pour n'importe quel type de Solitaire S ![]() Z2,
on définit alors la fonction linéaire
Z2,
on définit alors la fonction linéaire ![]() telle que :
telle que :
| : | ZS | G2 | ||
| ei,j | (g1(i,j), g2(i,j)) |
G2 est l'ensemble des 42=16 couples (g1,g2) : {(a,a),(a,b),(a,c),(a,e),(b,a),(b,b),(b,c),(b,e),(c,a),(c,b),(c,c),(c,e), (e,a),(e,b),(e,c),(e,e)}.
ei,j est le (i,j)ème vecteur unité dans RS,
c'est à dire que ei,j représente une configuration avec un seul pion dans la (i,j)ème position.
Par exemple :
| En conséquence, si P | = | (p1,p2,p3,...,pn-2,pn-1,pn) |
| = | (pi1,j1,pi2,j2,pi3,j3,...,pin-2,jn-2,pin-1,jn-1,pin,jn) et ek = eik,jk pour k = 1,...,n | |
| alors P | = | p1 e1 + p2 e2 + p3 e3 + ... + pn-2 en-2 + pn-1 en-1 + pn en |
| = | pi1,j1 ei1,j1 + pi2,j2 ei2,j2 + pi3,j3 ei3,j3 + ... + pin-2,jn-2 ein-2,jn-2 + pin-1,jn-1 ein-1,jn-1 + pin,jn ein,jn | |
| Et donc :
| = | |
| = | p1 |
|
| = | pi1,j1 |
|
| = |
Pour la configuration initiale du Solitaire anglais avec un pion au centre P0 = e0,0 = e17 :
| | = | (a,a) et pour le complémentaire de P0 : |
| | = | |
| = | |
|
| = | (c+a+b + b+c+a + b+c+a + b+c+a + b + a+b+c + b+c+a + c+a+b + c+a+b + c + a+b+c + c+a+b, c+a+b + a+b+c + c+a+b + c+a+b + c + a+b+c + b+c+a + b+c+a + b+c+a + b + b+c+a + c+a+b) |
|
| | = | (0 + 0 + 0 + 0 + b + 0 + 0 + 0 + 0 + c + 0 + 0, 0 + 0 + 0 + 0 + c + 0 + 0 + 0 + 0 + b + 0 + 0)=(b+c,c+b)=(a,a) |
La configuration pleine du Solitaire (tous les pions dans les trous) est définie par :
![]() (1)
(1)![]() (1,1,...,1)
(1,1,...,1)![]()
![]() (ei,j)
(ei,j)![]() (g1(i,j), g2(i,j))
(g1(i,j), g2(i,j))
![]() (1)
(1)![]() (P)
(P)![]() (P)
(P)
Donc pour le Solitaire anglais, ![]() (1)
(1)![]() (e0,0 + 1 - e0,0)
(e0,0 + 1 - e0,0)![]() (e0,0)
(e0,0)![]() (1 - e0,0)
(1 - e0,0)
Pour n'importe quel mouvement valide
| ou |
Ces dernières relations nous donnent la règle de trois d'après la définition de la faisabilité :
Une condition nécessaire à un couple de configuration (P,P') pour être faisable est que
![]() (P'-P) = (e,e)
(P'-P) = (e,e)![]() Ker(
Ker(![]() )
)![]() (P') =
(P') = ![]() (P)
(P)
En effet, on a :
| ==> | |
|
| ==> | |
|
| ==> | |
|
| ==> | |
Une application immédiate de la règle de trois au Solitaire anglais est que les seules configurations P à 32 pions pouvant aboutir à la configuration finale P'0 avec un pion au milieu sont ces 5 configurations :

De même, les seules configurations finales à 1 pion qui peuvent être faisable à partir de la configuration initiale P0 sont ces 5 configurations :

En effet toutes ces configurations sont les seules qui vérifient ![]() (P)=
(P)=![]() (P')=(a,a)
(P')=(a,a)
.gif)
Néanmoins, la règle de trois ne peut pas affirmer que (P0,P'0),
(P1,P'0), (P2,P'0), (P3,P'0),
(P4,P'0) et (P0,P'1), (P0,P'2),
(P0,P'3), (P0,P'4) soient faisables mais elle
affirme que tous les autres couples de configuration (P,P'0) et
(P0,P') ne sont pas faisables car ![]() (P)
(P)![]() (a,a)
(a,a)![]() (P')
(P')![]() (a,a)
(a,a)
On sait après calculs que ces 9 couples de configurations sont faisables :

Le nombre de solutions de ces 8 derniers couples de configuration est le quart du nombre de solution de (P0,P'0), car P0 a 4 choix possibles au premier mouvement alors que les plateaux P1, P2, P3, P4 n'ont qu'un seul choix au premier mouvement ainsi que P'1 P'2, P'3, P'4 avec des mouvements inversés : Leibnitz et le Solitaire inversé.
Une autre démonstration du problème de faisabilité des 5 configurations P'0, P'1, P'2, P'3, P'4 à partir de P0 se trouve ici :
http://www.cut-the-knot.com/ctk/RL-modes.html
| D'après la règle de trois : | (P,P') faisable | ==> | |
| Donc : | (P,P) faisable | ==> | |
| ==> | |
||
| (P,P) faisable | ==> | |
|
| (P,P) faisable | ==> | |
Cette dernière relation nous donne cette propriété :
Pour n'importe quel type de Solitaire S, une condition nécessaire pour qu'un couple de configurations (P,P) soit faisable
Une application immédiate de cette propriété est que tous les couples de configuration complémentaires (P,P) ne sont pas
faisables avec les types de Solitaire S vérifiant ![]() (1)
(1)![]() (e,e)
(e,e)
Et en effet, au Solitaire français, ![]() (1)=(a,a)
(1)=(a,a)![]() (e,e) :
(e,e) :

Au Solitaire français, il n'existe donc aucun chemin entre un plateau et son complémentaire et donc le jeu du Solitaire français classique consistant à partir du milieu pour arriver au milieu n'a pas de solution non plus (cf. ici pour une autre démonstration dans le cas du Solitaire français classique).
La règle de trois a quelques autres propriétés intéressantes comme savoir si une configuration quelconque P peut aboutir à une configuration P' avec un seul pion, quelque soit l'emplacement du pion.
Si P' est un plateau avec un seul pion,
![]() (P')
(P') ![]() {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)} :
{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)} :
(c,c).gif)
![]() (P')
(P') ![]() {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)}
{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)}
On en déduit que si ![]() (P) n'appartient pas à {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)},
(P,P') n'est pas faisable :
(P) n'appartient pas à {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)},
(P,P') n'est pas faisable :
Si P est un plateau quelconque et P' est un plateau avec un seul pion, il suffit
que ![]() (P) = (e,g)
(P) = (e,g)![]() (P)=(g,e)
(P)=(g,e)![]() G = {a,b,c,e}
G = {a,b,c,e}
De même, le problème complémentaire nous donne pour tous les types de Solitaire S où ![]() (1)=(e,e)
comme le Solitaire anglais avec P' un plateau avec un seul pion :
(1)=(e,e)
comme le Solitaire anglais avec P' un plateau avec un seul pion :
![]() (1 - P') =
(1 - P') = ![]() (1) -
(1) - ![]() (P') = (e,e) -
(P') = (e,e) - ![]() (P') =
(P') = ![]() (P') +
(P') + ![]() (P') -
(P') - ![]() (P') =
(P') = ![]() (P')
(P')
Donc tous les plateaux à n-1 pions (32 pions au Solitaire anglais) vérifient aussi :
![]() (1-P')
(1-P') ![]() {(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)}
{(a,a),(a,b),(a,c),(b,a),(b,b),(b,c),(c,a),(c,b),(c,c)}
Et donc les couples de configurations (P,P') avec P à n-1 pions et P' quelconque ne sont pas faisables
si ![]() (P')=(e,g)
(P')=(e,g)![]() (P')=(g,e)
(P')=(g,e)![]() G={a,b,c,e}.
G={a,b,c,e}.
| Fonctions en Pagode (armée infinie de pions) : |
Pour présenter les fonctions en Pagode, rien de mieux que le problème de l'armée infinie de pions illustré dans le Livre de John H. Conway.
Introduction en anglais : http://mathworld.wolfram.com/ConwaysSoldiers.html
Le plateau est tout l'espace Z2 (un plateau infini en quelque sorte).
On imagine le demi-plan inférieur rempli de pions :

On souhaite envoyer un pion éclaireur le plus haut possible.
Intuitivement, on pourrait penser qu'avec cette infinité de pions, on pourrait aller très haut :
Pour parvenir au niveau +1, 2 pions au minimum sont nécessaires (un pion est alors enlevé du plateau) :

Pour parvenir au niveau +2, 4 pions au minimum sont nécessaires (3 pions sont alors enlevés du plateau) :

Pour parvenir au niveau +3, 8 pions au minimum sont nécessaires (7 pions sont alors enlevés du plateau) :

A t-on besoin de 2n pions au minimum pour atteindre le niveau n :
Non, puisque pour parvenir au niveau +4, 20 pions au minimum sont nécessaires (19 pions sont alors enlevés du plateau) :

Correction du 22/01/06 : j'avais écris précédemment qu'il fallait 21 pions minimum et non 20 pour arriver au niveau +4 en l'illustrant avec le graphique suivant (qui est de mon point de vue la façon la plus simple d'arriver au niveau +4 mais c'était faux, je m'en suis aperçu en lisant la page : http://mathworld.wolfram.com/ConwaysSoldiers.html)

Et pour le niveau +5 ?
Le niveau +5 est inatteignable !
Démonstration :
Soit une fonction F(x,y) qui attribue un réel à tout emplacement rempli (x,y) du plateau.
Cette fonction est dite en Pagode si elle a la propriété que la somme de F(x,y) sur tous les emplacements avec des pions ne peut augmenter après un mouvement valide M.
Si on considère le mouvement valide M qui transforme le triplet T en T', on a M = T'-T.
Si on note F(T), la somme des F(x,y) sur le triplet T et M = T'-T, un mouvement valide :
on a F(M) = F(T'-T) = F(T') - F(T)
Soit (P,P') un couple de configurations de plateaux (P plateau initial, P' plateau final)
On note F(P) = ![]() F(x,y), somme sur tous les emplacements de P avec des pions.
F(x,y), somme sur tous les emplacements de P avec des pions.
et F(P') = ![]() F(x,y), somme sur tous les emplacements de P' avec des pions.
F(x,y), somme sur tous les emplacements de P' avec des pions.
Supposons que (P,P') soit faisable :
P' = P + ![]() Mi
Mi
La fonction F est donc en pagode si pour tout (P,P') faisable :
F(P') ![]() F(P)
F(P)
F(P + ![]() Mi)
Mi) ![]() F(P)
F(P)
![]() F(x,y) +
F(x,y) + ![]() F(Mi)
F(Mi) ![]()
![]() F(x,y)
F(x,y)
Donc si :
![]() F(Mi)
F(Mi) ![]() 0
0
En particulier si :
F(Mi) ![]() 0
0
On pose F(x,y)=s|x|+|y|, avec s réels à déterminer.
Vérifions que F(x,y) est une fonction en Pagode et pour quelles valeurs de s :Les valeurs prises par |x|+|y| dans la plan sont représentées par ce graphique :

Imaginons maintenant un mouvement M horizontal, il y a donc 3 cas :
Les mouvements à gauche du plan :

Les mouvements au milieu du plan :

Les mouvements à droite du plan :

En regroupant toutes ces inégalités et en remarquant que pour les mouvements verticaux, ces inégalités sur s sont identiques, on a :
(1) - sn+2 - sn+1 + sn ![]() 0
0
(2) sn+2 - sn+1 - sn ![]() 0
0
(3) sn ![]() 0
0
En sommant les 2 premières inégalités (1) et (2), on obtient :
sn+1 ![]() 0
0
donc s x sn ![]() 0
0
or d'après (3) sn ![]() 0
0
donc :
(3') s ![]() 0
0
(1) et (2) s'écrivent aussi :
sn (- s2 - s + 1) ![]() 0
0
sn ( s2 - s - 1) ![]() 0
0
Puisque d'après (3) sn ![]() 0
0
(1') - s2 - s + 1 ![]() 0
0
(2') s2 - s - 1 ![]() 0
0
Ou encore :
(1') s2 + s - 1 ![]() 0
0
(2') - s2 + s + 1 ![]() 0
0
(3') s ![]() 0
0
F(x,y) = s|x|+|y| est donc une fonction en Pagode si s appartient à l'intervalle : ![]()
On choisit s = ![]()
Remarque :
![]() est le nombre d'or
est le nombre d'or

s est la solution positive de l'équation s2 + s - 1 = 0 et
|s| a une valeur inférieure à 1, ce qui aura son importance pour avoir la convergence
de la série entière ![]() F(x,y) =
F(x,y) = ![]() s|x|+|y|
s|x|+|y|
Maintenant, considérons ce graphique en forme de Pagode inversée (c'est donc de là que vient le nom de fonctions en Pagode) :

L'origine (x,y)=(0,0) du Plan est au 5ème niveau qu'on souhaiterait atteindre.
Calculons la somme de F(x,y) sur le demi-plan inférieur (en dessous du niveau 0, niveau 0 compris) :
| ... | s10 | s9 | s8 | s7 | s6 | s5 | s6 | s7 | s8 | s9 | s10 | ... |
| ... | s10 | s9 | s8 | s7 | s6 | s7 | s8 | s9 | s10 | ... | ||
| ... | s10 | s9 | s8 | s7 | s8 | s9 | s10 | ... | ||||
| ... | s10 | s9 | s8 | s9 | s10 | ... | ||||||
| ... | s10 | s9 | s10 | ... | ||||||||
| ... | s10 | ... | ||||||||||
| ... |
![]() F(x,y) = s5 + 3 s6 + 5 s7 + 7 s8 + 9 s9 + 11 s10 + ... + (2 n + 1) sn+5 + ...
F(x,y) = s5 + 3 s6 + 5 s7 + 7 s8 + 9 s9 + 11 s10 + ... + (2 n + 1) sn+5 + ...
Cette série entière est égale à :

La série entière est donc bien convergente (Rayon de convergence égal à 1) avec s bien compris entre -1 et 1.


Donc :

Et donc :

![]() F(x,y) = s5 + 3 s6 + 5 s7 + 7 s8 + 9 s9 + 11 s10 + ... + (2 n + 1) sn+5 + ...
F(x,y) = s5 + 3 s6 + 5 s7 + 7 s8 + 9 s9 + 11 s10 + ... + (2 n + 1) sn+5 + ...
La configuration initiale P (tout le demi-plan inférieur) est telle que :
F(P) = ![]() F(x,y) = 1-
F(x,y) = 1-
Regardons les configurations finales P' qui ont au moins un pion au niveau 5 en (0,0) :
F(P') = ![]() F(x,y)
F(x,y) ![]()
![]() F(0,0) = s|0|+|0| = s0 = 1
F(0,0) = s|0|+|0| = s0 = 1
F(P') = ![]() F(x,y)
F(x,y) ![]() 1
1
F étant une fonction en pagode, (P,P') est faisable si :
F(P') ![]() F(P)
F(P)
or F(P) = 1- et F(P') ![]() 1
1
Donc F(P') > F(P)
Et donc les configurations (P,P') ne sont pas faisables.
Cette inégalité (introduite par cette Pagode inversée) prouve donc que le vecteur différence est à l'extérieur du cône du Solitaire et donc que les couples de configurations (P,P') sont infaisables.
Le niveau 5 est en conséquence inatteignable car quelque soit l'emplacement au 5ème niveau choisi
comme origine (0,0) dans le calcul, par translation à gauche ou a droite (sur l'abscisse x donc)
on obtient le même problème et donc le même résultat :
Soit P un plateau infini ayant le demi-plan inférieur rempli de pions :
Toutes les configurations (P,P') avec P' ayant au moins un pion au niveau 5 (et peut être ailleurs)
ne sont pas réalisables.
Remarque : s, s2, s3,..., sn
peuvent être mis sous cette forme également (suite de Fibonacci) :
s2 = - s + 1
s3 = s (s2) = - s2 + s = - (- s + 1) + s = 2 s - 1
s4 = s (s3) = s (2 s - 1) = 2 s2 - s = 2 (- s + 1) - s = - 3 s + 2
s5 = s (s4) = s (- 3 s + 2) = - 3 s2 + 2 s = -3 (- s + 1) + 2 s = 5 s - 3
s6 = s (s5) = s (5 s - 3) = 5 s2 - 3 s = 5 (- s + 1) - 3 s = - 8 s + 5
s7 = s (s6) = s (- 8 s + 5) = - 8 s2 + 5 s = -8 (- s + 1) + 5 s = 13 s - 8
..........................................................................................................
| Cône du Solitaire (fonctions en Pagode) : |
On a vu ici la définition de la faisabilité : (P,P') est faisable si P'-P est la somme de mouvements valides.
On va s'intéresser ici aux sommes de mouvements quelconques valides ou non, comme si on autorisait des nombres positifs et même négatifs de pions dans les trous.
On impose néanmoins que les mouvements doivent rester soustractifs, c'est à dire qu'on garde l'esprit du jeu initial : un mouvement entraîne un pion en moins ou plusieurs pions ici (pas comme Leibnitz et le Solitaire inversé). On refuse donc les mouvements additifs qui augmentent le nombre de pions a la place (cf. Lattice criterion (critère étendu de la règle de trois)).
On appelle le jeu original le jeu {0,1} dans le sens que toutes les configurations intermédiaires entre P et P' appartiennent à {0,1}S, c'est à dire que les configurations intermédiaires ont 0 ou 1 pion dans chaque trou. On dit alors que (P,P') est faisable ou {0,1}-faisable.
On s'intéresse ici au jeu entier ou Z-jeu dans le sens où toutes les configurations intermédiaires appartiennent à ZS, c'est à dire que les configurations intermédiaires ont alors un nombre entier positif ou négatif de pions dans chaque trou.
Par définition, on dit que (P,P') est Z-faisable si
P'-P ![]() ECS={
ECS={![]() ai Mi : ai
ai Mi : ai![]() N}
N}
Mi étant le ième mouvement des m mouvements valides de S (m=76 au solitaire anglais).
ECS est le cône entier du Solitaire, c'est à dire l'ensemble des combinaisons linéaires
de tous les mouvements valides avec des scalaires entiers non-négatifs.
On a alors cette proposition immédiate (cf. définition de la faisabilité) :
Une condition nécessaire pour qu'un couple de configuration (P,P') soit faisable est que
P'-P ![]() ECS.
ECS.
En effet si (P,P') est faisable, P'-P est décomposable en somme de mouvements valides inclue dans l'ensemble des combinaisons linéaires de mouvements (avec des entiers positifs) ECS.
On peut étendre l'ensemble des combinaisons linéaires de mouvements non plus avec des entiers positifs uniquement mais avec des réels positifs, on autorise alors en quelque sorte des configurations intermédiaires avec des fractions de pions négatives ou positives dans les trous. Ce jeu, on l'appelle le jeu fractionnel ou R-jeu puisque les configurations intermédiaires appartiennent alors toutes à RS.
Par définition, on dit que (P,P') est R-faisable si
P'-P ![]() CS={
CS={![]() ai Mi : ai
ai Mi : ai![]() R+}
R+}
Mi étant toujours le ième mouvement des m mouvements valides de S (m=76 au solitaire anglais).
CS est le cône du solitaire, c'est à dire l'ensemble des combinaisons linéaires
de tous les mouvements valides avec des scalaires réels non-négatifs (positifs ou nuls donc).
La terminologie du cône est empruntée de l'algèbre linéaire (et de la géométrie bien-sûr pour visualiser),
le cône étant un sous-ensemble de vecteurs C tel que si x ![]() C alors a x
C alors a x ![]() C pour tout a
C pour tout a ![]() R.
R.
De même que précédemment, on a alors la proposition immédiate importante (cf. définition de la faisabilité) :
Une condition nécessaire pour qu'un couple de configuration (P,P') soit faisable est que
P'-P ![]() CS.
CS.
En effet si (P,P') est faisable, P'-P est décomposable en somme de mouvements valides inclue dans l'ensemble des combinaisons linéaires de mouvements avec des entiers positifs ECS, ensemble lui-même inclus dans l'ensemble des combinaisons linéaires de mouvements avec des réels positifs CS :
Donc si (P,P') est faisable :
P'-P ![]() ECS
ECS ![]() CS
CS
Le but est alors de trouver des fonctions ou inégalités qui
démontrent que P'-P ![]() CS,
ce qui suffirait à prouver que (P,P') n'est pas faisable.
CS,
ce qui suffirait à prouver que (P,P') n'est pas faisable.
Ces inégalités vrais pour CS et fausses pour P'-P prouvent que (P,P') n'est
pas faisable.
Ces inégalités sont aussi appelées fonctions en Pagode :
Elles démontrent comme dans le problème de l'armée infinie de pions
que P'-P ![]() CS, le vecteur
P'-P est en dehors du cône du Solitaire et donc (P,P') est infaisable.
CS, le vecteur
P'-P est en dehors du cône du Solitaire et donc (P,P') est infaisable.
Pour cela, on définit les facettes de CS comme l'ensemble
des vecteurs f tel que le produit scalaire f.x soit négatif ou nul :
![]() 0 pour tout x
0 pour tout x ![]() CS
CS
En particulier, si x ![]() CS
et f est une facette de CS alors f.x
CS
et f est une facette de CS alors f.x ![]() 0.
0.
Et la contraposée donne donc :
Si f.x > 0 alors x ![]() CS
ou f n'est pas une facette de CS.
CS
ou f n'est pas une facette de CS.
Ou encore :
Si f.x > 0 avec f une facette de CS
alors x ![]() CS
CS ![]() ECS
ECS
![]() {0,1}S, c'est à dire
que x n'est pas {0,1}-faisable.
{0,1}S, c'est à dire
que x n'est pas {0,1}-faisable.
Si x=P'-P et f est une facette de CS, on a alors la fonction en Pagode ou l'inégalité f.(P'-P) > 0 qui traduit la non-faisabilité de (P,P') si l'inégalité est réalisée.
Exemple d'une facette f du Solitaire anglais :

Voici un couple de configurations (P,P') :
 infaisable (Pagoda).gif)
Calculons le produit scalaire f.(P'-P) :
Puisque f.(P'-P)>0, (P,P') n'est pas faisable.
Il faut donc calculer quelques facettes qui nous donnent directement des critères de non-faisabilité. On en a déjà une, en fait il en existe un très grand nombre pour ne pas dire une infinité.
Propriétés des facettes de CS :
Si x ![]() CS, on a vu
que x est de la forme :
CS, on a vu
que x est de la forme :
x = ![]() ai Mi ,ai
ai Mi ,ai![]() R+
R+
Par exemple, au Solitaire anglais on pourrait avoir : x = 1/2 (0,...,0,1,-1,-1) + 1/4 (0,...,0,-1,-1,1) + 1/3 (0,...,0,1,-1,-1,0,0,0) + 1/7 (0,...,0,-1,-1,1,0,0,0) + ... + 1/9 (1,-1,-1,0,...0) + 1/4 (-1,-1,1,0,...,0) : x est une combinaison linéaire de mouvements avec des réels positifs.
Soit ti le ième triplet du Solitaire S (p=38 triplets au Solitaire anglais avec 2 mouvements valides dans chaque triplet soit m=76 mouvements)
et ti,j sa jième composante sur les 3 composantes du triplet ti :
f.x ![]() 0 pour tout x
0 pour tout x ![]() CS
CS
si f.![]() ai Mi
ai Mi![]() 0 pour tout ai
0 pour tout ai![]() R+
R+
si ![]() ai f.Mi
ai f.Mi![]() 0 pour tout ai
0 pour tout ai![]() R+
R+
si a1t1.M1 + a2t1.M2 + a3t2.M3 + a4t2.M4 + ... + am-3tp-1.Mm-3 + am-2tp-1.Mm-2 + am-1tp.Mm-1 + amtp.Mm ![]() 0 pour tout ai
0 pour tout ai ![]() R+
R+
si a1(t1,1-t1,2-t1,3) + a2(-t1,1-t1,2+t1,3) + ... + am-1(tp,1-tp,2-tp,3) + am(-tp,1-tp,2+tp,3) ![]() 0 pour tout ai
0 pour tout ai ![]() R+
R+
puisque ti.Mj = (ti,1,ti,2,ti,3).(1,-1,-1) = ti,1 - ti,2 - ti,3
ou ti.Mj = (ti,1,ti,2,ti,3).(-1,-1,1) = -ti,1 - ti,2 + ti,3
suivant le sens du mouvement Mj dans le ième triplet ti (2 mouvements possibles dans chaque triplet).
Puisque tous les coefficients ai sont positifs ou nuls, la dernière inégalité est vraie en particulier si :
Pour tout i = 1,..,p :
| et - |
Donc il suffit que les p triplets ti (1 ![]() i
i ![]() p) d'une configuration f vérifient :
p) d'une configuration f vérifient :
| et - |
On vérifie par exemple que la facette f est bien une facette :

En effet tous les triplets vérifient :
11-8-3![]() 0 (11
0 (11![]() 8+3),
-11-8+3
8+3),
-11-8+3![]() 0 (3
0 (3![]() 11+8)
...
-1-0-(-1)
11+8)
...
-1-0-(-1)![]() 0 (-1
0 (-1![]() 0-1),
-(-1)-0-1
0-1),
-(-1)-0-1![]() 0 (-1
0 (-1![]() 0-1),
4-3-1
0-1),
4-3-1![]() 0 (4
0 (4![]() 3+1),
-4-3+1
3+1),
-4-3+1![]() 0 (1
0 (1![]() 3+4)
...
-1-0-(-1)
3+4)
...
-1-0-(-1)![]() 0 (-1
0 (-1![]() 0-1),
-(-1)-0-1
0-1),
-(-1)-0-1![]() 0 (-1
0 (-1![]() (0-1)
(0-1)
si t=(t1,t2,t3) est un triplet de f :
(1) t1 - t2 - t3 ![]() 0
0
(2) - t1 - t2 + t3 ![]() 0
0
Ces deux relations (1) et (2) peuvent être réunies en une seule :
-t1+t3![]() t1
t1![]() t2+t3
t2+t3
Propriétés des facettes issues des relations (1) et (2) :
Ce sous-ensemble de facettes F est intéressant dans la mesure où l'on peut fabriquer facilement un très grand nombre de facettes à partir de ces deux relations et de leurs implications :
En effet (1) + (2) donne la relation :
t1 - t2 - t3 - t1 - t2 + t3 ![]() 0
0
soit - 2 t2 ![]() 0
0
soit t2 ![]() 0
0
Ce qui signifie que la composante du milieu de tous les triplets de f n'est jamais négative :
Si f est une facette vérifiant (1) et (2) (donc une facette appartenant au sous-ensemble F), les composantes de f ne peuvent être négatives qu'aux extrémités du Solitaire.
De même si t2=0 avec (1) et (2), on a alors :
t1-t3![]() 0
0
-t1+t3![]() 0
0
soit t3![]() t1
t1![]() t3
t3
donc t1 = t3
Soit f une facette vérifiant (1) et (2), si pour un triplet (t1,t2,t3)
de f on a t2=0, alors :
t1 = t3
La conséquence immédiate de la dernière relation est :
Si deux entrées consécutives d'une rangée (ou d'une colonne)
ont la valeur 0 pour une facette vérifiant (1) et (2), alors toute les entrées de la rangée
(ou de la colonne) ont la valeur 0.
On peut donc calculer assez facilement des facettes, voici quelques facettes respectant toutes (1) et (2) :

On peut donc trouver autant de fonctions ou inégalités qu'il y a de facettes, c'est à dire beaucoup et autant de critères de non-faisabilité par la même.
| Lattice criterion (critère étendu de la règle de trois) : |
Nous avons autorisé dans le cône du Solitaire des nombres de pions positifs et négatifs dans les trous mais interdit des mouvements additifs (cf. Mouvements soustractifs et additifs). Ici, on autorise même les mouvements additifs, en enlevant la condition du signe (positif pour le cône du Solitaire) sur les scalaires ai :
Par définition, on dit que (P,P') est LS-faisable si
P'-P ![]() LS={
LS={![]() ai Mi : ai
ai Mi : ai![]() Z}
Z}
Mi étant le ième mouvement des m mouvements valides de S (m=76 au solitaire anglais).
LS est l'ensemble lattice, c'est à dire l'ensemble des combinaisons linéaires
de tous les mouvements valides avec des scalaires entiers négatifs, positifs ou nuls (des entiers donc).
On a alors cette proposition immédiate (lattice criterion) plus faible que celle pour le cône du Solitaire (cf. Proposition du cône entier du Solitaire) :
Une condition nécessaire pour qu'un couple de configuration (P,P') soit faisable est que
P'-P ![]() LS.
LS.
En effet si (P,P') est faisable, P'-P est décomposable en somme de mouvements valides inclue dans l'ensemble des combinaisons linéaires de mouvements (avec des entiers quelconques) LS.
On en déduit cette proposition importante :
Pour n'importe quel type de Solitaire S, on a cette relation : LS ![]() Ker(
Ker(![]() ).
).
Comme le montre ce graphique représentant LS et Ker(![]() ) :
) :

En effet :
v ![]() LS ==> v =
LS ==> v = ![]() ai Mi, ai
ai Mi, ai ![]() Z
Z
Donc pour tout v ![]() LS,
LS, ![]() (v) =
(v) = ![]() (
(![]() ai Mi) = ai
ai Mi) = ai ![]()
![]() (Mi)
(Mi)
Or on a vu que (cf. ici) : ![]() (Mi) = (e,e) pour tout Mi (mouvement valide).
(Mi) = (e,e) pour tout Mi (mouvement valide).
Donc pour tout v ![]() LS,
LS, ![]() (v) = (e,e)
(v) = (e,e)
Et donc ![]() (LS) = (e,e)
(LS) = (e,e)
Donc, si on a un couple de configuration (P,P') qui vérifie P'-P ![]() Ker(
Ker(![]() )
mais qui ne vérifie pas P'-P
)
mais qui ne vérifie pas P'-P ![]() LS, c'est à dire si P'-P
LS, c'est à dire si P'-P ![]() LS alors
(P,P') est infaisable.
LS alors
(P,P') est infaisable.
On voit ainsi que le Lattice criterion est plus fort que La règle de trois en général.
Néanmoins, le Lattice criterion et la La règle de trois
sont identiques pour le Solitaire anglais et le Solitaire français,
c'est à dire que LS = Ker(![]() ) dans ces deux cas (d'où l'inclusion large dans la proposition).
) dans ces deux cas (d'où l'inclusion large dans la proposition).
Pour le prouver et compléter le Lattice criterion, je vous renvois aux publications ici.
Vérifier l'appartenance de P'-P à LS est donc un problème plus simple
que vérifier l'appartenance de P'-P à CS :
on le voit très bien avec le solitaire anglais et français où il suffit de calculer
![]() (P) et
(P) et ![]() (P')
pour savoir si P'-P
(P')
pour savoir si P'-P ![]() Ker(
Ker(![]() ) = LS.
) = LS.
Pour l'appartenance de P'-P à CS, c'est un problème plus difficile
où les fonctions en Pagode sont utiles mais il existe des méthodes pour savoir
si P'-P ![]() CS (de même pour ECS).
CS (de même pour ECS).
Pour prouver la non-faisabilité de Solitaires en général, l'appartenance de P'-P à
CS ![]() LS est souvent suffisante.
En effet il faut que P'-P
LS est souvent suffisante.
En effet il faut que P'-P ![]() CS
et que P'-P
CS
et que P'-P ![]() LS pour que (P,P') soit faisable.
LS pour que (P,P') soit faisable.
C'est à dire que P'-P ![]() CS
CS ![]() LS.
LS.
Donc le complémentaire donne :
Il suffit que P'-P ![]() CS
ou que P'-P
CS
ou que P'-P ![]() LS pour que (P,P') soit infaisable.
LS pour que (P,P') soit infaisable.
C'est à dire que P'-P ![]() CS
CS ![]() LS.
LS.
Par exemple pour le couple de configurations (P,P') suivant infaisable (déjà vu ici) :
 infaisable (Pagoda).gif)
P'-P ![]() Ker(
Ker(![]() ) = LS
) = LS
mais P'-P ![]() CS (cf. ici)
CS (cf. ici)
De même, pour cette configuration suivante infaisable (Solitaire français) :

P'-P ![]() Ker(
Ker(![]() )=LS (cf. Solitaires français complémentaires)
)=LS (cf. Solitaires français complémentaires)
mais P'-P ![]() CS :
CS :
Il suffit de trouver une décomposition en somme de P'-P appartenant à CS pour le prouver
ou alors et c'est plus simple de prouver qu'il existe bien au moins une décomposition (avec la méthode du
simplexe par exemple) et c'est le cas ici :
cf. méthodes pour déterminer l'ensemble où P'-P appartient
D'ailleurs, puisque P'-P ![]() CS,
on voit immédiatement que les fonctions en Pagode ne sont d'aucune utilité pour le
cas classique du Solitaire français (du milieu au milieu) puisque bien sûr les fonctions en Pagode
essayent de prouver quand elles le peuvent que P'-P
CS,
on voit immédiatement que les fonctions en Pagode ne sont d'aucune utilité pour le
cas classique du Solitaire français (du milieu au milieu) puisque bien sûr les fonctions en Pagode
essayent de prouver quand elles le peuvent que P'-P ![]() CS
donc l'inverse !
CS
donc l'inverse !
Mais ça n'a pas d'importance puisque La règle de trois est capable elle de déterminer
la non-faisabilité du problème.
Pour finir, on a ECS ![]() CS
CS ![]() LS,
CS
LS,
CS ![]() LS est donc un ensemble plus grand que ECS donc moins intéressant que
ECS pour montrer la non-faisabilité si il y a.
LS est donc un ensemble plus grand que ECS donc moins intéressant que
ECS pour montrer la non-faisabilité si il y a.
L'ensemble ECS (sommes des mouvements avec des entiers positifs) est clairement inclus dans l'intersection de l'ensemble CS (sommes des mouvements avec des réels positifs) avec l'ensemble LS (sommes des mouvements avec des entiers relatifs) :
En effet :
ECS ![]() CS
CS
ECS ![]() LS
LS
Donc :
ECS ![]() CS
CS ![]() LS
LS
Mais c'est bien une inclusion stricte :
Par exemple, le couple de configurations (P,P') ci-dessous (jeux de Solitaire à 7 pions) est
LS-faisable (P'-P ![]() LS)
et aussi R-faisable (P'-P
LS)
et aussi R-faisable (P'-P ![]() CS)
mais pas Z-faisable (P'-P
CS)
mais pas Z-faisable (P'-P ![]() ECS)
ECS)
P'-P = (1,0,0,0,0,0,1) - (1,1,0,1,0,1,1) = (0,-1,0,-1,0,-1,0)
En effet, par exemple :
2(-1,-1,1,0,0,0,0) - 1.(0,-1,-1,1,0,0,0) - 1.(0,0,-1,-1,1,0,0) - 1.(0,0,0,-1,-1,1,0) + 0.(0,0,0,0,-1,-1,1)
+ 2.(1,-1,-1,0,0,0,0) + 2.(0,1,-1,-1,0,0,0) + 0.(0,0,1,-1,-1,0,0) + 0.(0,0,0,1,-1,-1,0) + 0.(0,0,0,0,1,-1,-1)
= (-2,-2,2,0,0,0,0) + (0,1,1,-1,0,0,0) + (0,0,1,1,-1,0,0)= + (0,0,0,1,1,-1,0) + (0,0,0,0,0,0,0) +
(2,-2,-2,0,0,0,0) + (0,2,-2,-2,0,0,0) + (0,0,0,0,0,0,0) + (0,0,0,0,0,0,0) + (0,0,0,0,0,0,0)
= (-2+2, -2+1-2+2, 2+1+1-2-2, -1+1+1-2, -1+1, -1, 0)
= (0,-1,0,-1,0,-1,0)
= P'-P
Donc avec a=(a1,a2,...,am-1,am) = (2,-1,-1,-1,0,2,2,0,0,0) (m=10 mouvements ici) :
P'-P = ![]() ai Mi : ai
ai Mi : ai![]() Z
Z
Et donc P'-P ![]() LS et (P,P') est LS-faisable.
LS et (P,P') est LS-faisable.
De même (seule solution dans CS) :
1/2(-1,-1,1,0,0,0,0) + 0.(0,-1,-1,1,0,0,0) + 1/2.(0,0,-1,-1,1,0,0) + 0.(0,0,0,-1,-1,1,0) + 1/2.(0,0,0,0,-1,-1,1)
+ 1/2.(1,-1,-1,0,0,0,0) + 0.(0,1,-1,-1,0,0,0) + 1/2.(0,0,1,-1,-1,0,0) + 0.(0,0,0,1,-1,-1,0) + 1/2.(0,0,0,0,1,-1,-1)
= (-1/2,-1/2,1/2,0,0,0,0) + (0,0,0,0,0,0,0) + (0,0,-1/2,-1/2,1/2,0,0) + (0,0,0,0,0,0,0) + (0,0,0,0,-1/2,-1/2,1/2) +
(1/2,-1/2,-1/2,0,0,0,0) + (0,0,0,0,0,0,0) + (0,0,1/2,-1/2,-1/2,0,0) + (0,0,0,0,0,0,0) + (0,0,0,0,1/2,-1/2,-1/2)
= (1/2-1/2, -1/2-1/2, 1/2-1/2-1/2+1/2, -1/2-1/2, 1/2-1/2-1/2+1/2, -1/2-1/2, 1/2-1/2)
= (0,-1,0,-1,0,-1,0)
= P'-P
Donc avec a=(a1,a2,...,am-1,am) = (1/2,0,1/2,0,1/2,1/2,0,1/2,0,1/2) (m=10 mouvements ici) :
P'-P = ![]() ai Mi : ai
ai Mi : ai![]() R
R
Et donc P'-P ![]() CS et (P,P') est RS-faisable.
CS et (P,P') est RS-faisable.
Pour montrer que P'-P ![]() ECS
et la façon dont on a trouvé les ai de a=(a1,a2,...,am-1,am) dans les
deux cas précédents, reportez vous à ce qui suit :
Analyse du Solitaire à 7 cases
ECS
et la façon dont on a trouvé les ai de a=(a1,a2,...,am-1,am) dans les
deux cas précédents, reportez vous à ce qui suit :
Analyse du Solitaire à 7 cases
Donc on a en particulier :
P'-P ![]() LS
LS
P'-P ![]() CS
CS
soit : P'-P ![]() CS
CS ![]() LS
LS
or : P'-P ![]() ECS
ECS
Et donc en général (du moins pour le Solitaire à 7 cases mais c'est vrai aussi pour les autres) :
ECS ![]() CS
CS ![]() LS
LS
D'où l'inclusion stricte (et non large) :
ECS ![]() CS
CS ![]() LS
LS
| Méthodes pour déterminer l'ensemble où P'-P appartient : |
Si on note FS l'ensemble des sommes de mouvements valides pour un type
de Solitaire S (Solitaire anglais au autre), on peut représenter les ensembles
CS,
LS, CS ![]() LS, ECS et FS
comme dans la figure ci-dessous.
(L'appartenance de P'-P a l'ensemble FS ne signifie pas pour autant que (P,P')
soit faisable mais simplement que pour chaque élément e de FS, il existe au moins un couple
de configurations (P,P') faisable tel que P'-P=e) :
LS, ECS et FS
comme dans la figure ci-dessous.
(L'appartenance de P'-P a l'ensemble FS ne signifie pas pour autant que (P,P')
soit faisable mais simplement que pour chaque élément e de FS, il existe au moins un couple
de configurations (P,P') faisable tel que P'-P=e) :

La non-appartenance de P'-P à ECS est donc la meilleure preuve que (P,P') est infaisable, c'est aussi la chose la plus difficile a calculer.
On pourra se contenter de calculer l'appartenance ou non de P'-P à
CS ![]() LS :
LS :
L'appartenance ou non de P'-P à LS s'obtient avec la La règle de trois au Solitaire français et anglais comme on a déjà vu.
La non-appartenance de P'-P à CS peut s'obtenir avec les inégalités sur le cône du Solitaire (Fonctions en Pagode).
Mais on peut calculer ces appartenances avec des méthodes plus coûteuse et quelque soit le type de Solitaire S envisagé.
Avant d'étudier précisément ces méthodes, voici quelques petites propriétés trouvées un peu par hasard en utilisant ces méthodes :
Si P'-P = ![]() ai Mi : ai
ai Mi : ai![]() R (vrai par exemple si (P,P') est faisable ou P'-P
R (vrai par exemple si (P,P') est faisable ou P'-P ![]() FS ou P'-P
FS ou P'-P ![]() CS ou P'-P
CS ou P'-P ![]() ECS ou P'-P
ECS ou P'-P ![]() LS) :
LS) :
P'-P = a1 M1 + a2 M2 + ... + am-1 Mm-1 + am Mm (m mouvements)
P'-P = a1 (-1,-1,1,0,...,0) + a2 (1,-1,-1,0,...,0) + a3 (0,-1,-1,1,0,...,0) + a4 (0,1,-1,-1,0,...,0) + ... + am-3 (0,...,0,-1,-1,1,0) + am-2 (0,...,0,1,-1,-1,0) + am-1 (0,...,0,-1,-1,1) + a4 (0,...,0,1,-1,-1)
Et donc si Pi est la ième composante de P (0 si pas de pion dans la case, 1 sinon) :
![]() P'i - Pi
= a1 (-1-1+1) + a2 (1-1-1) + a3 (-1-1+1) + a4 (1-1-1) + ... + am-3 (-1-1+1) + am-2 (1-1-1) + am-1 (-1-1+1) + am (1-1-1)
P'i - Pi
= a1 (-1-1+1) + a2 (1-1-1) + a3 (-1-1+1) + a4 (1-1-1) + ... + am-3 (-1-1+1) + am-2 (1-1-1) + am-1 (-1-1+1) + am (1-1-1)
![]() P'i - Pi
= - a1 - a2 - a3 - a4 - ... - am-3 - am-2 - am-1 - am
P'i - Pi
= - a1 - a2 - a3 - a4 - ... - am-3 - am-2 - am-1 - am
![]() P'i - Pi = -
P'i - Pi = - ![]() ai
ai
Ou encore :
![]() ai =
ai = ![]() Pi -
Pi - ![]() P'i
P'i
![]() Pi est le nombre de pions de P présents sur les n cases.
Pi est le nombre de pions de P présents sur les n cases.
![]() Pi -
Pi - ![]() P'i est donc le nombre de mouvements pour aller de P à P' (32-1=31 mouvements dans le cas classique du Solitaire anglais).
P'i est donc le nombre de mouvements pour aller de P à P' (32-1=31 mouvements dans le cas classique du Solitaire anglais).
Si P'-P peut se décomposer sous la forme P'-P = ![]() ai Mi (ai
ai Mi (ai ![]() R)
alors la somme des coefficients ai est égale au nombre de mouvements nécessaires pour aller de P à P' :
R)
alors la somme des coefficients ai est égale au nombre de mouvements nécessaires pour aller de P à P' :
![]() =
= ![]() Pi -
Pi - ![]() P'i
P'i
De plus, Admettons que (P,P') soit faisable avec un nombre de pions de P inférieur au nombre de pions de P' (ce qui est évidemment
absurde mais c'est justement une démonstration par l'absurde) alors :
![]() Pi <
Pi < ![]() P'i
P'i
![]() Pi -
Pi - ![]() P'i < 0
P'i < 0
Et donc puisque (P,P') est faisable par hypothèse, P'-P est décomposable et donc :
![]() ai < 0
ai < 0
donc il n'existe pas de décomposition P'-P = ![]() ai Mi : ai
ai Mi : ai![]() N (
N (![]() ai serait supérieur ou égal à zéro sinon)
ai serait supérieur ou égal à zéro sinon)
et P'-P ![]() ECS
ECS
et donc (P,P') n'est pas faisable.
En conclusion, (P,P') ne peut pas être faisable si le nombre de pions de P est inférieur au nombre de
pions de P', ce que nous savions évidemment déjà, c'était juste une petite démonstration supplémentaire :
(P,P') faisable ==> ![]() Pi -
Pi - ![]() P'i
P'i ![]() 0
0
Si P'-P est décomposable avec ai ![]() 0 (vrai par exemple pour CS, ECS et FS) alors :
0 (vrai par exemple pour CS, ECS et FS) alors :
0 ![]() ai
ai ![]()
![]() ai =
ai = ![]() Pi -
Pi - ![]() P'i
P'i
0 ![]() ai
ai ![]()
![]() Pi -
Pi - ![]() P'i
P'i
Ce qui signifie que le nombre de mouvements identiques Mi à un certain endroit du Solitaire S qui est représenté par ai est toujours
inférieur ou égal au nombre de mouvements nécessaire pour aller de P à P' (et est positif ou nul) :
c'est encore une fois évident, et cette limite est de loin inférieur au Solitaire anglais ou français. Il serait intéressant de calculer les 76 limites des 76 mouvements valides du Solitaire anglais. En fait, avec les symétries et rotations, 16 calculs de ces limites suffisent pour calculer les 76 :

En tout cas, avec les méthodes qui suivent, on peut se poser ce genre de question :
Le couple de configurations (P,P') a t-il des solutions avec au moins ai mouvements identiques
à tel ou tel endroit ?
Du moins, on peut vérifier plus exactement que (P,P') n'a pas de solution avec plus de a1 mouvements identiques à un certain endroit, a2 mouvements identiques à un autre, etc... mais on ne peut pas affirmer qu'il y a des solutions (ce sont toujours des critères de non-faisabilité et non de faisabilité).
Analyse du Solitaire à 7 cases :
On va d'abord étudier le Solitaire à 7 cases (n=7) vu déjà ici (pour simplifier le problème) :
Ce solitaire a donc 10 mouvements valides (m=10) : {(-1,-1,1,0,0,0,0),(0,-1,-1,1,0,0,0), (0,0,-1,-1,1,0,0),(0,0,0,-1,-1,1,0),(0,0,0,0,-1,-1,1),(1,-1,-1,0,0,0,0),(0,1,-1,-1,0,0,0), (0,0,1,-1,-1,0,0),(0,0,0,1,-1,-1,0),(0,0,0,0,1,-1,-1)}
On utilise une matrice Mn,m où le nombre de ligne est égal au nombre de case n et le nombre de colonne est égal aux nombre de mouvements m (n=7 et m=10).
Les vecteurs générateurs M1,...,M10 (mouvements valides vu ci-dessus) sont les vecteurs colonnes de cette matrice.
Donc la matrice Mn,m pour le Solitaire à 7 cases est la suivante :

On cherche à résoudre P'-P = ![]() ai Mi, ai
ai Mi, ai ![]() R.
R.
Matriciellement, si A=(a1,a2,...,am-1,am) et B=P'-P, on a :
M.A = B
Il suffit donc de calculer l'ensemble des vecteurs A vérifiant cette égalité et de voir si il existe des vecteurs solution où toutes leurs composantes appartiennent à R+ pour CS ou à N pour ECs ou à Z pour Ls.
On pourra utilisé la méthode du simplexe pour le calcul sur CS (bien plus rapide), les calculs sur les autres ensembles sont des calculs de programmation entière qu'il sera intéressant d'optimiser par la suite.
Analyse du Solitaire à 7 cases par Mapple
Téléchargez le fichier Mapple (format MWS) : solitaire7.mws
>
restart;
>
with(linalg) :
Warning, new definition for norm
Warning, new definition for trace
>
M:=matrix(7,10,[[-1,0,0,0,0,1,0,0,0,0],[-1,-1,0,0,0,-1,1,0,0,0],[1,-1,-1,0,0,-1,-1,1,0,0],[0,1,-1,-1,0,0,-1,-1,1,0],[0,0,1,-1,-1,0,0,-1,-1,1],[0,0,0,1,-1,0,0,0,-1,-1],
[0,0,0,0,1,0,0,0,0,-1]]);
![[Maple Math]](mapple7/Solitaire71.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Analyse du Solitaire anglais (n=33 cases) :
C'est exactement pareil que pour le solitaire à 7 cases sauf qu'il faut ajouter les triplets verticaux.
Ce solitaire a 76 mouvements valides (m=76).
On utilise toujours une matrice Mn,m (n=33 et m=76).
Les vecteurs générateurs M1,...,M76 (mouvements valides) sont les vecteurs colonnes de cette matrice.
Donc la matrice Mn,m pour le Solitaire anglais est la suivante :

Analyse du Solitaire anglais (33 cases) par Mapple
Téléchargez le fichier Mapple (format MWS) : solitaire33.mws
>
restart;
>
with(linalg):
Warning, new definition for norm
Warning, new definition for trace
>
>
# (P,P2) est le couple de configurations classique du solitaire anglais : "milieu vers milieu"
>
P:=vector(33,[1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]);
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| Critère des extrémités du Solitaire : |
Une extrémité ou un coin est un emplacement qui a exactement un emplacement voisin horizontal et un emplacement voisin vertical.
Par exemple, les extrémités du Solitaire anglais sont ces 8 emplacements :

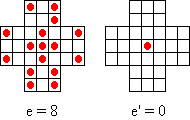
Si on note E, l'ensemble des extrémités, et e le nombre de pions présents aux extrémités dans une configuration P, on a la propriété suivante :
(P,P') est faisable si on peut enlever e-e' pions dans E.
Par exemple, il faut enlever 8-0=8 pions aux extrémités ici :
On divise l'ensemble E en deux ensembles Eh et Ev comme ceci :

(P,P') est faisable si on peut enlever eh-eh' pions dans Eh et ev-ev' dans Ev.
Pour enlever les eh-eh' pions de Eh, il faut eh-eh' pions appartenant à S (cf. Critères des ensembles jouables) pour que les pions aux extrémités se retrouvent dans ces 4 emplacements :

De même, pour enlever les ev-ev' pions de Ev, il faut ev-ev' pions appartenant à T (cf. Critères des ensembles jouables) pour que les pions aux extrémités se retrouvent dans les 4 emplacements précédents.
Pour supprimer un pion d'une extrémité, il doit passer par un de ces 4 emplacements. Pour arriver à ces emplacements, on a besoin d'autant de pions appartenant à S (ou T pour Ev) que de pions aux extrémités pour réaliser les sauts.
On peut aussi se retrouver par exemple dans cette configuration où l'on passe par une extrémité voisine mais le problème reste inchangé, le pion de T utilisé pour faire le saut (ou S pour Ev) n'influence pas le critère :

Il faut encore un pion restant au minimum appartenant à S ou T pour supprimer le pion ou les pions se trouvant alors parmi ces 4 emplacements (un seul pion de S ou T peut très bien éliminer les 4 pions à la fois si la configuration le permet mais il en faut au moins un) :

En utilisant les notations S,T,s et t (cf. Critères des ensembles jouables) :
Et donc :
Ce qui nous intéresse ce sont les critères de non faisabilité donc le complémentaire ou l'inverse
des ces deux formulations.
La deuxième formulation a alors deux avantages :
1) la présence de quatre inégalités à la place des six égalités et inégalités de la première formulation
2) des inégalités liées par des et logique qui ont donc comme
complémentaires des ou logique qui ont l'avantage qu'une seule inégalité peut faire
la décision sur la non faisabilité d'un couple de configurations.
Il suffit que :
| s<eh-eh' | |
| ou | s-(eh-eh')+t |
| ou | t<ev-ev' |
| ou | s-(ev-ev')+t |
Ce critère de non faisabilité est d'autant plus intéressant que le nombre d'extrémités est important. Ainsi, le Solitaire français qui a 12 extrémités ou la version continentale avec 16 extrémités sont mieux adaptés pour ce critère que le solitaire anglais et ses 8 extrémités.
On peut d'ailleurs trouver des relations similaires avec d'autres pions que ceux aux extrémités du Solitaire.
| Critère des extrémités du Solitaire (problème complémentaire) : |
Une configuration (P,P') est faisable si sa configuration complémentaire (P',P) l'est aussi.
Il suffit donc d'appliquer le critère précédent avec le couple de configuration (P',P) à la place de (P,P') pour avoir un nouveau critère de non-faisabilité.
Ce critère est en quelque sorte le critère complémentaire du critère précédent, néanmoins les résultats de ces 2 critères (complémentaires ou non) peuvent très bien être différents : l'un peut très bien déterminer qu'une configuration (P,P') n'est pas faisable alors que l'autre ne peut rien conclure.
Le problème complémentaire avec les autres critères revient au même que le problème initial donc il est inutile de tester les couples (P',P) à partir des couples (P,P') pour La règle de trois ou les autres critères.
| Critères des ensembles jouables : |
Au Solitaire, on peut partitionner les différents emplacements des pions du plateau dans des ensembles disjoints formant k classes d'équivalence qui ont la propriété de réunir les emplacements jouables par un même pion.
En effet, les pions peuvent être déplacé que dans certains emplacements durant toute leur durée de vie, ainsi un pion à un emplacement (i,j) ne pourra par exemple jamais atteindre l'emplacement d'un de ces voisin, mais pourra atteindre uniquement les emplacements espacés de 2 modulo 2 (écart multiple de 2).
La relation liant les même pions d'une partition (classe) est donc cette propriété de déplacement interne dans la partition.
Au solitaire anglais, il existe 4 partitions ou classes (k=4) qu'on nomme S, T, M et C pour reprendre les notations du programme de Philippe Basciano :

Le nombre d'éléments dans S,T,M et C au Solitaire anglais est donc :
Pour une configuration P, on note s,t,m et c les nombres de pions présents dans S,T,M et C respectivement
![]() 8,t
8,t![]() 8,m
8,m![]() 5,c
5,c![]() 12).
12).
Au Solitaire anglais, le nombre de mouvements maximum que l'on peut obtenir avec un seul et même pion (dit balayage) est de 16 mouvements dans la classe C (c=0) comme cette figure le montre :

Cliquez ici pour plus de détails
La propriété vraiment intéressante des ensembles jouables sur la faisabilité de (P,P') est qu'il doit y avoir un nombre de pions dans chaque classe S,T,M,C de P supérieur ou égal au nombre de pions dans chaque classe de P' respectivement pour que (P,P') soit faisable.
En effet, si on se retrouvait avec une configuration d'arrivée P' avec plus de de pion dans C (par exemple) qu'avec la configuration de départ, on pourrait immédiatement affirmer que (P,P') est infaisable car les c pions de C dans P ne peuvent engendrer plus de pions dans C et donc pas les c' pions de C dans P' si c'>c :

Cette configuration (P,P') n'est donc pas faisable.
Avec des mouvements valides, le nombre de pions ne peut que diminuer ou rester inchangé dans un même ensemble (classe S,T,M ou C).
On en déduit ces critères de non faisabilité (critères des ensembles jouables) :
Soient s,t,m,c et s',t',m',c' les nombres de pions dans les ensembles S,T,M,C pour P et P' respectivement.
Il suffit que :
| s'>s | |
| ou | t'>t |
| ou | m'>m |
| ou | c'>c |
| Critères de non faisabilité triviaux : |
Si un couple de configuration (P,P') passe à travers tous ces critères de non faisabilité, ce couple n'est pas pour autant faisable, il faut recommencer avec les successeurs de P (ou les prédécesseurs de P' si l'on souhaite remonter l'arbre plutôt que de le descendre). Toutefois, afin d'accélérer la procédure, on peut choisir les successeurs (ou prédécesseurs) les plus pertinents en utilisant une heuristique ou un choix probabiliste comme dans la méthode de Pascal Glauser (algorithme génétique), où l'on utilise le fait que la probabilité de gagner est plus grande quand les pions des plateaux intermédiaires sont plus densifiés vers la solution (on peut utiliser les barycentres ou le coloriage du plateau par des poids pour simplifier) : voir ici.
Une fois l'arbre élagué par tous ces critères, on pourra affirmer que (P,P') est faisable si on a trouvé un chemin particulier allant de P à P'.
Si on ne trouve pas de chemins valides après avoir parcouru l'arbre élagué entièrement, on pourra affirmer que (P,P') n'est pas faisable : la vérification peut être longue avec des Solitaires plus grands que le Solitaire anglais (Solitaire français par exemple, qui).
| Solutions du Solitaire français : |
Le Solitaire français n'a hélas pas de solution en partant du milieu pour arriver au milieu (cf. Solitaires français complémentaires).
Voici une autre démonstration dérivée de la la règle de trois :

On colorie le plateau du Solitaire français par les trois couleurs {a,b,c}.
On considère les 3 fonctions suivantes :
a(n) = (nombre de pions d'un plateau ayant la couleur a après un nombre de mouvements valides n) modulo 2
b(n) = (nombre de pions d'un plateau ayant la couleur b après un nombre de mouvements valides n) modulo 2
c(n) = (nombre de pions d'un plateau ayant la couleur c après un nombre de mouvements valides n) modulo 2
x modulo 2 représente le reste de la division de x par 2 (congruence modulo 2), c'est à dire que :
si x est pair, x modulo 2 = 0 (x congru à 0)
si x est impair, x modulo 2 = 1 (x congru à 1)

Au Solitaire français (37 cases), entre la configuration P (36 pions) et la configuration P' (1 pion), il nécessite donc
a(0), b(0), c(0) sont les nombres de pions modulo 2 pour la configuration initiale P (pas encore de mouvement)
a(1), b(1), c(1) sont les nombres de pions modulo 2 après le premier mouvement
...........................................................................................................................
a(35), b(35), c(35) sont les nombres de pions modulo 2 pour la configuration finale P' (dernier mouvement)
Calculons le nombres de pions de couleurs a, b et c pour la configuration initiale P :
12 pions de couleur a pour P
12 pions de couleur b pour P
12 pions de couleur c pour P
Donc :
a(0) = 12 modulo 2 = 0
b(0) = 12 modulo 2 = 0
c(0) = 12 modulo 2 = 0
Le premier mouvement quel qu'il soit fait perdre 2 pions de couleurs b et c et gagner un pion de couleur a :
Donc a(1) = 13 modulo 2 = 1
Donc b(1) = 11 modulo 2 = 1
Donc c(1) = 11 modulo 2 = 1
On s'aperçoit donc qu'un mouvement valide quelconque fait varier a(n), b(n) et c(n) de la valeur 0 à 1
ou de la valeur 1 à 0 et ce quel que soit n (0 ![]() n
n ![]() 35)
35)
Et donc a(n + 1), b(n + 1) et c(n + 1) passent à 1 quand a(n), b(n) et c(n) sont à 0 et inversement a(n + 1), b(n + 1) et c(n + 1) passent à 0 quand a(n), b(n) et c(n) sont à 1.
Ce qui s'écrit d'ailleurs si a(0) = b(0) = c(0) = 0 :
a(n + 1) + a(n) = 1 : a(n + 1) = 1 - a(n)
b(n + 1) + b(n) = 1 : b(n + 1) = 1 - b(n)
c(n + 1) + c(n) = 1 : c(n + 1) = 1 - c(n)
(0 ![]() n
n ![]() 35)
35)
On a donc :
a(2 p) = 0
a(2 p + 1) = 1
b(2 p) = 0
b(2 p + 1) = 1
c(2 p) = 0
c(2 p + 1) = 1
(0 ![]() p
p ![]() 17)
17)
Ou encore :
a(n) = 0 si n est pair
a(n) = 1 si n est impair
b(n) = 0 si n est pair
b(n) = 1 si n est impair
c(n) = 0 si n est pair
c(n) = 1 si n est impair
(0 ![]() n
n ![]() 35)
35)
On peut donc calculer a(35), b(35) et c(35) :
a(35) = b(35) = c(35) = 1 (35 est impair)
Hors P' n'a qu'un pion de couleur a !
Et donc b(35) et c(35) devraient avoir la valeur 0 si le couple de configurations (P,P') était faisable
(décomposable en mouvements valides).
Le Solitaire français n'a donc pas de solution (milieu vers milieu).
Pourtant on jouait au XVIIIème siècle à ce jeu et j'imagine que la princesse de Soubise n'était pas assez stupide pour jouer à un jeu sans solution.
En effet, Frans CREMERS, un instituteur à la retraite d'Aalter, en Belgique, a trouvé la clef de la solution. En fait, il a découvert comment la version originelle était jouée au XVIIIème siècle :
Le pion de départ n'est pas réellement pris, il peut être remis
ultérieurement. C'est au joueur de décider quand il souhaite
le remettre à sa place.
Voila comment on y jouait :
Démarrez avec 37 pions, enlevez un pion,
mettez-le de coté et remettez le plus tard dans le trou
où vous l'avez pris.
Source : http://www.users.skynet.be/sol.france/nouv.htm
Il y a donc des solutions mais je ne les ai pas comptabilisées,
n'ayant pas vraiment traité le Solitaire français.
| Solutions du Solitaire anglais : |
Des solutions particulières, vous en trouverez sur plusieurs sites comme sur celui de Frederic DOS SANTOS :
http://www.chez.com/Solitaire/solut_1.htm
http://www.chez.com/Solitaire/solut_2.htm
J'ai calculé en 1997-1998 le nombre exact de chemins distincts aboutissant à la solution du Solitaire anglais (partir du milieu pour arriver au milieu).
|
|
Ce résultat a été vérifié et publié aussi par Frédéric DOS SANTOS sur son site :
http://www.chez.com/Solitaire
J'ai ensuite calculé le nombre total de chemins du Solitaire anglais dans le but d'évaluer une probabilité de gagner au Solitaire.
|
|
Tout d'abord la répartition des solutions n'est pas du tout équiprobable, c'est à dire qu'il existe des zones à très forte densité en solutions et des zones totalement vides.
Donc le calcul d'une telle probabilité n'a pas vraiment de sens car un tel nombre ne représente pas la probabilité de gagner en jouant au hasard mais seulement la proportion de chemins gagnants par rapport à l'ensemble des chemins réalisables (en partant du milieu).
D'ailleurs ce nombre si vous le calculez :

Vous voyez, ça ferait environ une chance sur 14124 de gagner au Solitaire anglais mais ça ne veut pas dire pour autant que vous trouverez une solution en jouant au hasard après 14124 tentatives (vérifier avec un ordinateur en tirant au hasard des chemins).
Par contre, si vous avez une solution, vous pouvez trouver d'autres solutions assez proches facilement en parcourant par exemple l'ensemble des chemins sur un plateau intermédiaire qui a mené à la solution lorsqu'il ne reste que quelques pions sur ce plateau (moins de 16). C'est aussi une façon de trouver des solutions en jouant d'abord jusqu'à un plateau intermédiaire (de 16 pions par exemple) qui semble pertinent (avec des pions regroupés vers le centre par exemple) et d'ensuite calculer l'ensemble des chemins à partir de ce plateau. On peut également le faire à l'envers, à partir de la solution et remonter jusqu'à un plateau intermédiaire et laisser l'ordinateur calculer les chemins inverses entre le plateau intermédiaire et la position de départ qu'on a choisi.
Au sujet de trouver une solution avec l'aide des probabilités , Pascal Glauser (voir son site http://homepage.sunrise.ch/homepage/pglaus/Solitaire/solitaire.htm) utilise une méthode basée sur l'affectation de poids aux cases du jeu en fonction de la distance de ces cases par rapport au centre du jeu et ceci afin d'augmenter la probabilité de trouver une solution en constatant justement que les plateaux où les pions sont regroupés vers le centre du jeu et répartis symétriquement ont plus de chance d'aboutir à une solution que les plateaux avec des pions répartis aux extrémités du jeu par exemple.
Pascal Glauser a d'ailleurs utilisé un algorithme génétique pour trouver des solutions sur ce principe que vous pouvez tester en ligne sur son site.
Il a affecté des poids par coloriage sur les cases du jeu en fonction de l'éloignement des cases par rapport au centre du jeu : poids identiques pour les cases symétriques par rapport à l'axe horizontal, vertical ou diagonal.
Ces poids permettent d'augmenter la probabilité de gagner en favorisant les plateaux ayant des pions plus proches du centre du jeu en moyenne.
Pour cela, on peut utiliser la représentation suivante où les cases sont différenciées suivant qu'elles sont symétriques ou non, par rapport à l'axe horizontal, vertical ou diagonal :
| A | B | A | ||||
| C | D | C | ||||
| A | C | E | F | E | C | A |
| B | D | F | G | F | D | B |
| A | C | E | F | E | C | A |
| C | D | C | ||||
| A | B | A |
On peut ensuite donner une valeur aux cases (poids), en fonction de l'éloignement par rapport au centre, ce qui donne par exemple, la représentation suivante où le centre a un poids égal à 1 :
| 8 | 7 | 8 | ||||
| 6 | 5 | 6 | ||||
| 8 | 6 | 3 | 2 | 3 | 6 | 8 |
| 7 | 5 | 2 | 1 | 2 | 5 | 7 |
| 8 | 6 | 3 | 2 | 3 | 6 | 8 |
| 6 | 5 | 6 | ||||
| 8 | 7 | 8 |
Si un pion est dans une case, il aura le poids associé a cette case. Ce poids représente la distance symbolique entre le pion et le centre du jeu. La somme des poids de tous les pions présents sur un plateau représente la distance symbolique de tous les pions par rapport au centre, nous l'appellerons le poids du plateau.
Donc, plus un plateau est léger, plus ses pions sont proches du centre, le poids du plateau le plus léger étant égal à 0 (aucun pion), le poids du plateau avec un seul pion au centre étant égal à 1, etc...
On peut également utiliser les barycentres avec les coordonnées du jeu centré en (0,0) et les vecteurs poids associés sur les cases, ce qui permettrait d'avoir le poids du plateau calculé avec la somme des normes (distances) des vecteurs, ainsi que le centre de gravité des pions du plateau calculé avec la somme des vecteurs poids divisée par le nombre de pions.
On choisit les plateaux successeurs où la densité des pions est plus importante au centre du jeu (plateau léger) et où le centre de gravité des pions est proche du centre du jeu (plateau équilibré). On peut imaginer pour cela un plateau posé en équilibre en son centre sur une aiguille où le barycentre des pions se rapproche du centre à mesure que le plateau s'allège. Du fait de la concentration des pions au centre, le plateau s'allège tout en s'équilibrant car les pions se retrouvent entre eux en symétries horizontales, verticales ou diagonales plus facilement : par exemple, 2 pions en symétrie centrale sont en équilibre, 3 pions appartenant à un triangle équilatérale inscrit dans un cercle (symétries verticales et diagonales) sont en équilibres, 4 pions appartenant à un carré inscrit dans un cercle (symétries horizontales et verticales) sont en équilibres, etc... Remarquons toutefois que le dernier coup gagnant au solitaire anglais n'est pas réalisé sur un plateau équilibré (exemple du triplet du style (101) équilibré mais sans solution), mais est réalisé sur un plateau non équilibré avec un quintuplet du style (11000) ou (00011), ce qui pourrait retarder la découverte de solutions dans un algorithme de parcours en profondeur du graphe utilisant les critères ci-dessus.
Important : il existe une solution complémentaire à toute solution !
| Solutions Complémentaires du Solitaire : |
Vous avez remarqué que le plateau de départ (32 pions sans celui du milieu) était l'inverse, l'opposé ou le complémentaire (comme vous voulez) du plateau d'arrivée (1 pion au milieu seulement).
Imaginez que vous jouez un coup avec la configuration de départ ou initial du Solitaire : de 32 pions, il reste alors 31 pions.
Faites le complémentaire des 4 coups jouables du départ : Vous retrouvez les 4 coups possibles terminant le Solitaire. Jusque la c'est normal vous me direz.
Continuez le processus avec 30 et 3 pions, 29 et 4 pions,..., 17 et 16 pions (milieu du jeu).
On voit alors que l'ensemble des plateaux à 17 pions, atteints après avoir commencé du départ a pour complémentaire l'ensemble des plateaux à 16 pions où pour chacun de ces plateaux à 16 pions, il existe au moins un chemin aboutissant à une solution.
Et le nombre exact de chemins menant à un plateau à 17 pions est égal au nombre de chemins d'un plateau à 16 pions aboutissant à la solution si ces deux plateaux (16 et 17 pions) sont complémentaires (car les chemins seraient donc complémentaires aussi dans ce cas et leurs nombres identiques par symétrie)
De plus, sur les :

Seule une petite fraction de ces Solitaires (plateaux) aboutissent à la solution (plateau final) :
Mais a quoi servent ces histoires de complémentaires me diriez vous ?
On en conclut que chaque chemin menant à une solution a un chemin complémentaire qui mène aussi à une autre solution.
Si vous avez trouvé une solution, vous en avez trouvé deux en fait, sans oublier que d'autres solutions sont généralement très proches.
| Solutions minimales du Solitaire anglais : |
Voila là encore, un challenge qui a été résolu dès 1912 par Ernest Bergholt.
John Beasley a prouvé que la solution de Ernest Bergholt était minimale en 1964.
| Livre de John D. Beasley : |
Je vous conseille le livre référence du Solitaire de John Beasley même si je ne l'ai pas lu car malheureusement le tirage est écoulé. (out of print comme disent nos amis Anglo-Saxons).
John Beasley, The Ins and Outs of Peg Solitaire, 275 pages, 1985, ISBN 0-19-853203-2
Oxford University Press

| Solution minimale ? |
Mais qu'est ce qu'une solution minimale ?
C'est tout simplement une solution où l'on a utilisé un maximum de fois les mêmes pions à la suite.
Par exemple si un des 4 pions que vous choisissez au début sautait tous les autres pions pour finalement atteindre le trou central, ce serait une solution minimale on ne peut plus minimale.
Mais au Solitaire anglais, ce cas n'est vraiment pas possible (on n'est pas aux Dames où l'on avale tous les pions adverses à la fin avec le pion promu Dame).
| Solution minimale d'Ernest Bergholt : |
Voici la solution minimale d'Ernest Bergholt :


Les couleurs violettes et bleues mettent en évidence les pions joués ou à jouer, l'alternance de ces couleurs mettant-elles en évidence le nombre de coups joués à la suite par un même et unique pion.
1 : 46x44
2 : 65x45
3 : 57x55
4 : 54x56
5 : 52x54
6 : 73x53
7 : 43x63
8 : 75x73x53
9 : 35x55
10 : 15x35
11 : 23x43x63x65x45x25
12 : 37x57x55x53
13 : 31x33
14 : 34x32
15 : 51x31x33
16 : 13x15x35
17 : 36x34x32x52x54x34
18 : 24x44
Vous remarquez qu'il y a 18 lignes.
Une ligne représente un balayage, c'est à dire un mouvement d'un pion qui capture un certain nombre d'autres pions (1 ou plusieurs). John Beasley a justement prouvé qu'il n'y avait pas moins de 18 balayages dans une solution au Solitaire anglais. Cette solution est donc minimale.Philippe Basciano dit que cette preuve a été donnée par Berkeley, un pseudonyme pour W. H. Peel : lisez le livre et envoyez-moi un mail si vous avez la réponse à : eternitygames@free.fr
46x44 signifie que le pion en ligne 4 et colonne 6 va dans le trou en ligne 4 et colonne 4. (le trou du milieu bien-sûr)
75x73x53 signifie que le pion en ligne 7 et colonne 5 va d'abord dans le trou en ligne 7 et colonne 3 puis en ligne 5 et colonne 3.
Vous voyez alors pourquoi on parle de solution minimale : c'est la plus petite façon de représenter une solution, les "x" évitant les redondances.
C'est aussi le chemin le plus rapide pour atteindre une solution bien-sûr puisqu'on garde le même pion plus longtemps.
| Nombre de solutions minimales du Solitaire anglais : |
Il existe d'autres solutions aussi minimales que
celle-ci, Sidney Cadot les a même toutes calculées.
Il m'a précisé qu'il existe 936 solutions minimales différentes
comme son graphe l'indique (cliquer sur l'image pour aller sur le site) :

Il semble donc qu'aucune solution minimale possède en plus un balayage plus grand que les 6 comptabilisés dans la première solution minimale d'Ernest Bergholt :
D'ailleurs, on pourrait calculer aussi les solutions ayant les plus longs balayages sans qu'elles soient forcément minimales :
On sait d'ailleurs grâce au résultat des 18 balayages minimums à toute solution que le balayage le plus long dans toute solution est inférieur ou égal à 15 (32-18+1).
Ce résultat doit être bien inférieur à 15 je suppose, alors si quelqu'un connaît le résultat...
On avait vu ici que le balayage le plus long au solitaire anglais
est de 16, ce qui signifie que ce balayage est inatteignable à partir du départ et/ou
que ce balayage n'atteint pas lui-même l'arrivée (maximum de 15 mouvements dans une solution).
En fait dans ce cas-ci, ce balayage n'est ni atteignable ni n'atteint la solution :
CF. La règle de trois et Critère des extrémités du Solitaire (problème complémentaire).
| Procédures pour calculer les successeurs (ou prédécesseurs) d'un plateau : |
Quand j'ai commencé à réfléchir sur le solitaire en 1996, je ne soupçonnais pas du tout ce qui se cachait derrière ce jeu qui parait plus simple qu'il n'est vraiment.
Je pensais au début qu'une simple exploration
du graphe du solitaire me permettrait de trouver
une solution particulière :
Il n'en est rien en fait comme je l'ai dis plus haut car
le graphe est bien trop grand.
(Il faudrait élaguer l'arbre pour le réduire et ainsi
trouver des solutions particulières en utilisant les critères vus
ici
et les symétries/Rotations du jeu).
Mais comme je n'avais pas encore l'Internet à cette époque ni aucune information sur ce jeu, je me suis lancé sans théorie ni rien, et le Solitaire m'a ainsi appris beaucoup de choses.
Je ne connaissais pas encore les graphes et encore
moins leurs théories (cf. théorie des graphes) à ce moment
(et même après avoir trouver le nombre de Solutions du Solitaire anglais d'ailleurs),
mais intuitivement les explorations de graphes
m'étaient déjà familières car je les utilisais sans le savoir
dans des programmes précédents comme celui pour résoudre Le compte est bon.
Si vous ne connaissez pas les graphes, voir plus bas des détails et un exemple.
A l'époque, j'avais donc fait de l'exploration en profondeur du graphe une priorité et ainsi le calcul des successeurs d'un plateau devait être le plus rapide possible.
Pour trouver les successeurs d'un plateau, il suffit de regarder les 76 triplets horizontaux et verticaux vérifiant la suite binaire 110 ou 011 (0 = un trou, 1 = un pion).
Soit reg64 un registre sur 64 bits représentant binairement le plateau du solitaire :
On peut utiliser l'instruction machine
Pour les prédécesseurs, il faut trouver les suites binaires 001 ou 100.
Pour calculer un plateau successeur ou un plateau prédécesseur, on inverse la suite binaire trouvée correspondante :
On pourra utiliser un
Exemple de programme pour tester et inverser les triplets (Assembleur) :
| SUB reg64,011B | ; on soustrait reg64 de 011B | |
| TEST reg64,111B | ; on teste les 3 bits | |
| JZ TRIPLET_A1 | ; si les 3 bits sont nuls, on va à TRIPLET_A1 | |
| SUB reg64,110B-011B | ; on soustrait reg64 (initial !) de 110B | |
| TEST reg64,111B | ; etc. | |
| JZ TRIPLET_B1 | ||
| SUB reg64,011000B-110B | ||
| RETOUR_TRIPLET_A2: | ||
| TEST reg64,111000B | ||
| JZ TRIPLET_A2 | ||
| ...................... | ||
| TRIPLET_A1: | ||
| ADD reg64,011B-011000B | ; anticipe le calcul du test suivant | |
| ; (remet reg64 initial et met à 0 les 3 bits suivants) | ||
| PUSH RETOUR_TRIPLET_A2 | ; enregistre sur la pile l'adresse de retour | |
| PUSH reg64 | ; enregistre sur la pile reg64 | |
| ADD reg64,011000B-011B+100B | ; on inverse les 3 bits par addition | |
| ........................... |
| SUB reg64,000000010000001000000B ; idem sauf que les bits sont alors espacés dans la représentation | |
| TEST reg64,100000010000001000000B | |
| JZ TRIPLET_A20 | |
| SUB reg64,100000010000000000000B-000000010000001000000B | |
| TEST reg64,100000010000001000000B | |
| JZ TRIPLET_B20 | |
| SUB reg64,0000000100000010000000B-100000010000000000000B | |
| RETOUR_TRIPLET_A21: | |
| TEST reg64,1000000100000010000000B | |
| JZ TRIPLET_A21 | |
| ........................................................ | |
| TRIPLET_A20: | |
| ADD reg64,000000010000001000000B-0000000100000010000000B | |
| PUSH RETOUR_TRIPLET_A21 | |
| PUSH reg64 | |
| ADD reg64,0000000100000010000000B-000000010000001000000B+100000000000000000000B | |
| ............................................................................... |
Tout ceci est bien lourd pour de simples tests mais c'est rapide et c'était le but que je m'étais fixé au tout début. J'utilisais deux registres de 32 bits pour codés les 33 bits du solitaire mais le deuxième registre (ou 33ème bit donc) était décalé dans le premier uniquement pour traiter les 4 cas particuliers où le 33ème bit était nécessaire dans les tests des triplets (mais maintenant autant utiliser les registres de 64 bits).
D'ailleurs, en utilisant de la mémoire vive, j'ai même fait beaucoup plus compliqué mais c'était vraiment pour le plaisir :
Alors qu'il est logique d'utiliser une représentation du solitaire comme celle-ci (représentation normale utilisée plus haut où les pions 1 à 33 sont codés dans une suite binaire de 33 bits) :

On peut compliquer la représentation dans le but d'optimiser
la recherche des successeurs (ou prédécesseurs).
Les successeurs sont précalculés dans
la mémoire vive mais pas complètement puisque la mémoire
ne permet pas d'enregistrer tous les successeurs
des 233 différents plateaux du Solitaire !
On utilise cette représentation horizontale et verticale à 2 fois 21 bits qui va permettre de passer d'un bloc à 21 bits à l'autre rapidement :

Les 33 bits du solitaire sont donc ordonnés suivant qu'on s'intéresse aux plateaux successeurs horizontaux ou verticaux.
On calculera auparavant dans la mémoire vive l'ensemble
des successeurs de tous les blocs de 21 bits.
Sur les 221 différents plateaux à
21 bits
On a donc besoin de 45 MO (ou 33 MO), ce qui est conséquent mais de moins en moins puisqu'on trouve aujourd'hui des ordinateurs avec 256 MO de RAM.
D'ailleurs sachant qu'il y a 15 successeurs au maximum pour un bloc
de 21 bits, on peut répartir l'ensemble des successeurs
sur 128 MO, 16x4 octets utilisés pour représenter les successeurs
de chaque plateau de 21 bits.
On a alors plus besoin que d'un seul
accès à la mémoire vive pour avoir un successeur à la place de deux
comme plus haut (table d'adresses + table des successeurs).
Pour passer d'un bloc de 21 bits horizontal à un plateau du solitaire normal (33 bits), on colle les 12 bits verticaux qui restent.
Voila une structure possible du solitaire (33 bits) :

Pourquoi cette représentation ?
Parce qu'il faut pouvoir traiter les blocs verticaux
en passant d'un plateau à 33 bits (solitaire) à un bloc vertical
sur 21 bits et inversement.
L'astuce est de faire une rotation sur les 8 premiers bits (carré central sans le pion central) pour passer d'un bloc horizontal (21 bits) à un bloc vertical (21 bits) et inversement pour finalement revenir à un plateau (33 bits).
On fait une rotation à droite de 2 unités pour passer d'un bloc horizontal à un bloc vertical et une rotation à gauche pour l'inverse.
Je rappelle que pour faire une rotation binaire (bitwise rotation en anglais), on dispose des instructions en assembleur ROL, ROR, RCL et RCR (RCL et RCR très utiles pour gérer un 33ème bit dans CF par exemple) ; à ne pas confondre avec SAL, SAR, SHR, SHLD et SHRD utilisés plus fréquemment mais pour le décalage binaire (en langage C, pour simplifier, ce sont les fonctions "rotl()" ou "rotr()" pour la rotation binaire à gauche ou à droite et les opérateurs "<<" ou ">>" pour le décalage binaire à gauche ou à droite).
Le pion central n'a pas besoin d'être tourné étant déjà au centre, c'est pour quoi il est éloigné de ses voisins dans la représentation.
On pourra calculer les successeurs et prédécesseurs avec la
même table de précalculs.
Si la table représente les successeurs (par exemple), on peut
trouver les prédécesseurs grâce à cette formule :

Logique vous me direz :
Le complémentaire d'un successeur d'un plateau complémenté
est un prédécesseur du plateau !
On ajoute deux instructions XOR pour calculer les complémentaires et on a ainsi les prédécesseurs à la place des successeurs.
Voilà en ce qui concerne la recherche des successeurs,
une simple boucle de 10 lignes en C aurait suffit
mais pourquoi faire simple quand on peut faire compliqué ?
Surtout quand le gain en vitesse est important !
| Graphe du Solitaire : |
| Graphe orienté sans circuit (GOSC) : |
Le Solitaire est un Graphe Orienté Sans Circuit (GOSC, dag en anglais pour directed acyclic graph) :

Un circuit est un chemin dont les deux extrémités coïncident (c'est donc un cycle orienté).
Un GOSC peut présenter de nombreux cycles, mais par sa définition même, on ne peut jamais tomber sur un circuit si l'on suit les arcs dans la direction indiquée.
Le Solitaire n'est pas un arbre car il possède des cycles (cf. figure) mais un GOSC ressemble à une arborescence et particulièrement le Solitaire qui est presque un arbre.
Tout graphe peut être défini par sa matrice d'adjacence M qui est une matrice carrée booléenne (que des 0 et des 1). L'existence d'un arc entre P et P' se traduit par la présence d'un 1 à l'intersection de la ligne P et de la colonne P' de la matrice M ; l'absence d'arc, par la présence d'un 0.
Le solitaire anglais ayant 233 combinaisons d'emplacements de pions sur le plateau, cette matrice carrée M a donc 233 lignes et colonnes et donc 266 éléments, autant dire qu'elle n'est pas représentable même par un ordinateur (pour l'instant).
| Chemins de longueur k et Fermeture transitive : |
Chemins de longueur k :
En théorie des graphes, pour calculer l'ensemble des chemins de longueur k entre chaque couple de sommets (P,P') du graphe, on élève à la puissance k la matrice d'adjacence M du graphe (on peut le prouver par récurrence sur k).
M représente les chemins de longueur 1
M2 représente les chemins de longueur 2
M3 représente les chemins de longueur 3
.............................................................
Mk représente les chemins de longueur k
Au Solitaire, Mi = 0 pour tout i ![]() n-1
(donc M32 = 0 au Solitaire anglais : n = 33 emplacements).
n-1
(donc M32 = 0 au Solitaire anglais : n = 33 emplacements).
Dans le graphe du Solitaire, on a cette propriété :
Si il existe au moins un chemin de longueur k entre un somment P et P',
alors il n'existe pas de chemin de longueur inférieure ou supérieure à k entre P et P'.
En effet, si il y a k mouvements entre le plateau P et P' (chemin de longueur k) alors le nombre de pions de P est égal au nombre de pions de P' + k. Si k est inférieur ou supérieur, il n'y donc aucun chemin transformant P en P'.
Ce qui se traduit en notant ![]() (x) l'ensemble des successeurs du sommet x :
(x) l'ensemble des successeurs du sommet x :
{x} ![]()
![]() (x)
(x)
![]()
![]() 2(x)
2(x) ![]() ...
... ![]()
![]() k(x)
k(x) ![]() ... =
... = ![]()
![]() 2(x) est l'ensemble des successeurs des successeurs de x
2(x) est l'ensemble des successeurs des successeurs de x
![]() 3(x) est l'ensemble des successeurs des successeurs des successeurs de x
3(x) est l'ensemble des successeurs des successeurs des successeurs de x
...............................................................................................................
Défini par la relation de récurrence :
![]() (x) =
(x) = ![]() (x) et
(x) et ![]() k(x) =
k(x) = ![]() (
(![]() k-1(x))
k-1(x))
Ce qui se traduit matriciellement :
si Mk(i,j) ![]() 0
alors Mi(i,j) = 0 pour tout i
0
alors Mi(i,j) = 0 pour tout i ![]() k.
k.
C'est à dire que si on considère la somme S = M + M2 + M3 + ... + Mk, chaque élément de la matrice S(i,j) appartient soit à M ou M2 ou ... ou Mk : la somme est donc une réunion en quelque sorte.
La somme S = M + M2 + M3 + ... = ![]() Mi = M + M2 + M3 + ....+ Mn-2
traduit le nombre de chemins entre chaque couple de sommets (P,P')
Mi = M + M2 + M3 + ....+ Mn-2
traduit le nombre de chemins entre chaque couple de sommets (P,P')
Avec la méthode de Horner : S =![]() Mi = M(I + M(I + M(...(I + M))))
Mi = M(I + M(I + M(...(I + M))))
Au solitaire anglais S =![]() Mi = M + M2 + M3 + ... + M31
(on s'arrête à n-2=31 car il n'y a pas de chemin de longueur supérieur à 31)
Mi = M + M2 + M3 + ... + M31
(on s'arrête à n-2=31 car il n'y a pas de chemin de longueur supérieur à 31)
Mk = 0 pour tout k ![]() n-1 : la matrice est nilpotente d'indice n-1.
n-1 : la matrice est nilpotente d'indice n-1.
M31 a par exemple 332 = 1089 composantes possiblement non-nulles, les
autres composantes étant nulles :
Il y a ![]() plateaux P avec 32 pions :
plateaux P avec 32 pions : ![]() = 33
= 33
Il y a ![]() plateaux P' avec 1 pion :
plateaux P' avec 1 pion : ![]() = 33
= 33
Donc il existe 332 = 1089 couples de sommets (P,P') qui ont des chemins de longueur 31 quand ils existent.
De plus, les éléments de la matrice M + M2 + ... + M30
sont nuls pour ces 1089 couples.
On peut organiser la matrice M comme ceci (Solitaire anglais) :

p = k représente l'ensemble des plateaux à k pions, k ![]() 32 au Solitaire anglais (0 pion et 33 pions n'ont pas d'intérêt au Solitaire anglais).
32 au Solitaire anglais (0 pion et 33 pions n'ont pas d'intérêt au Solitaire anglais).
p = 16 représente l'ensemble des plateaux à 16 pions par exemple.
M représente les chemins de longueur 1 : d'où les triangles de valeur nulle le long de la diagonale.
La matrice M² devient alors :

M2 représente les chemins de longueurs 2 : les triangles de valeur nulle le long de la diagonale sont alors plus grands.
........................................................
Mn-2 = M31 = 0 (au Solitaire anglais)
La matrice S = M + M² + ... peut donc être représenté comme ceci :

Remarque :
Le nombre total de chemins à partir de P est la somme des éléments de la ligne dans la matrice M correspondant à P.
Le nombre total de chemins se terminant à P' est la somme des éléments de la colonne dans la matrice M correspondant à P'.
Le nombre total de chemins global est la somme de tous les éléments de la matrice M (somme de toutes les lignes ou de toutes les colonnes de la matrice M).
Fermeture transitive d'un graphe :
La Fermeture transitive F d'un graphe est une version simplifiée de S =![]() Mi :
Mi :
S =![]() Mi donne le nombre de chemins entre P et P'
Mi donne le nombre de chemins entre P et P'
F donne l'existence ou non d'un chemin entre P et P', c'est à dire que F est une matrice booléenne.
Remarque :
Il suffit de remplacer dans S tous les éléments supérieurs ou égaux à 1 par 1 justement pour avoir la
fermeture transitive F.
Si on considère F(x) la Fermeture transitive d'un sommet x sur le graphe, on a l'expression :
F(x) = {x} ![]()
![]() (x)
(x)
![]()
![]() 2(x)
2(x)
![]() ...
... ![]()
![]() n-2(x)
n-2(x)
La Fermeture transitive s'obtient en utilisant comme loi additive, la somme logique ![]() (ou logique)
et comme loi multiplicative, le produit logique (et logique) :
(ou logique)
et comme loi multiplicative, le produit logique (et logique) :

La matrice M[k] est la matrice M à la puissance k en tenant compte des ces 2 lois : c'est donc aussi une matrice booléenne (comme M).
M[k] représente donc l'existence ou non de chemins de longueur k entre P et P'.
La Fermeture transitive représente l'existence ou non de chemins entre P et P' (longueur quelconque) donc :
F = I ![]() M
M ![]() M[2]
M[2] ![]() M[3]
M[3] ![]() ...
... ![]() M[n-2]
M[n-2]
Au solitaire, on s'arrête à n-2 pour les mêmes raisons que pour la matrice S.
On obtient la matrice F plus simplement avec cette formule :
F = (I ![]() M)[n-2]
M)[n-2]
En effet, la formule du binôme de Newton donne à cause de l'idempotence de la somme booléenne :
(1 ![]() 1 = 1) :
1 = 1) :
(A ![]() B)[n] = A[n]
B)[n] = A[n] ![]() A[n-1].B
A[n-1].B ![]() A[n-2].B[2]
A[n-2].B[2] ![]() ...
... ![]() B[n]
B[n]
Et donc :
(I ![]() M)[n-2] = I[n-2]
M)[n-2] = I[n-2] ![]() I[n-3].M
I[n-3].M ![]() I[n-4].M[2]
I[n-4].M[2] ![]() ...
... ![]() M[n-2] =
I
M[n-2] =
I ![]() M
M ![]() M[2]
M[2] ![]() M[3]
M[3] ![]() ...
... ![]() M[n-2] = F
M[n-2] = F
Pour calculer F, on peut remarquer que :
| F | = (I |
| = (I | |
| = (I | |
| = (I |
Donc au Solitaire anglais par exemple :
F = (I ![]() M)[31] = (I
M)[31] = (I ![]() M)[32]
M)[32]
et (I ![]() M)[32] est rapide à calculer car
32 est une puissance de 2 :
M)[32] est rapide à calculer car
32 est une puissance de 2 :
On calcule :
(I ![]() M)[2] = (I
M)[2] = (I ![]() M).(I
M).(I ![]() M)
M)
(I ![]() M)[4] = (I
M)[4] = (I ![]() M)[2].(I
M)[2].(I ![]() M)[2]
M)[2]
(I ![]() M)[8] = (I
M)[8] = (I ![]() M)[4].(I
M)[4].(I ![]() M)[4]
M)[4]
(I ![]() M)[16] = (I
M)[16] = (I ![]() M)[8].(I
M)[8].(I ![]() M)[8]
M)[8]
(I ![]() M)[32] = (I
M)[32] = (I ![]() M)[16].(I
M)[16].(I ![]() M)[16]
M)[16]
On a donc besoin de 5 multiplications matricielles.
Pour calculer F, il existe aussi l'algorithme de Roy-Warshall plus rapide mais nécessitant quand même 299 opérations rien qu'au solitaire anglais ! (complexité en O(n3), n=233 sommets)
Algorithme de Roy-Warshall :
1. F ![]() M
M
2. pour i = 1 à n faire
3. F(i,i) ![]() 1
1
4. pour k = 1 à n faire
5. pour j = 1 à n faire
6. pour i = 1 à n faire
7. F(i,j) ![]() F(i,j) ou ( F(i,k) et F(k,j) ) (qui équivaut à : F(i,j)
F(i,j) ou ( F(i,k) et F(k,j) ) (qui équivaut à : F(i,j) ![]() F(i,j)
F(i,j) ![]() F(i,k) x F(k,j) )
F(i,k) x F(k,j) )
Pour calculer S, on peut aussi utiliser l'algorithme de Roy-Warshall (car la matrice M est nilpotente) en l'adaptant aux sommes et multiplications
habituelles (même complexité alors que pour F).
La méthode de Horner vue plus haut est plus longue.
Algorithme de Roy-Warshall adapté :
1. S ![]() M
M
2. pour i = 1 à n faire
3. S(i,i) ![]() 1
1
4. pour k = 1 à n faire
5. pour j = 1 à n faire
6. pour i = 1 à n faire
7. S(i,j) ![]() S(i,j) + S(i,k) x S(k,j)
S(i,j) + S(i,k) x S(k,j)
Remarque :
On peut aussi retrouver S à partir de (I + M)k = I + k M + ... + k Mk-1 + Mk
(au Solitaire anglais, on calcule (I + M)32, k=32 car 32 est une puissance de 2 pour les mêmes raisons que précédemment)
On obtient S = I + M + M2 + ... en enlevant I de (I + M)k, ensuite en divisant par
k tous les éléments de la zone de (I + M)k correspondant à M (chemins de longueur 1),
en divisant par k (k-1) / 2 tous les éléments de la zone de (I + M)k correspondant à M2 (chemins de longueur 2)
, ..., en divisant par k (k-1) / 2 tous les éléments de la zone de (I + M)k correspondant à Mk-1 (chemins de longueur k-1),
en divisant par k tous les éléments de la zone de (I + M)k correspondant à Mk (chemins de longueur k) :
au solitaire anglais on s'arrête à k - 1 = 31.
La matrice S =![]() Mi (ainsi que la Fermeture transitive F =
Mi (ainsi que la Fermeture transitive F =![]() M[i]) peuvent être calculé aussi en appliquant sur les n sommets P du graphe
(233 au Solitaire anglais) un algorithme déterminant tous les descendants du sommet P
(calcul moins grand en tenant compte des symétries et des propriétés des complémentaires).
M[i]) peuvent être calculé aussi en appliquant sur les n sommets P du graphe
(233 au Solitaire anglais) un algorithme déterminant tous les descendants du sommet P
(calcul moins grand en tenant compte des symétries et des propriétés des complémentaires).
La matrice S =![]() Mi (ainsi que la Fermeture transitive F =
Mi (ainsi que la Fermeture transitive F =![]() M[i]) étant bien trop grandes pour être calculées actuellement, ce sont des algorithmes
déterminant l'ensemble des descendants d'un sommet P (problème d'accessibilité en théorie des graphes)
qui vont nous permettre de calculer rapidement le nombre de solutions du Solitaire anglais et le nombre total de chemins
à partir du sommet initial (pion au milieu).
M[i]) étant bien trop grandes pour être calculées actuellement, ce sont des algorithmes
déterminant l'ensemble des descendants d'un sommet P (problème d'accessibilité en théorie des graphes)
qui vont nous permettre de calculer rapidement le nombre de solutions du Solitaire anglais et le nombre total de chemins
à partir du sommet initial (pion au milieu).
L'étape suivante serait donc de calculer la matrice S =![]() Mi
(ou la Fermeture transitive
Mi
(ou la Fermeture transitive ![]() M[i]
M[i]
| Algorithmes pour calculer le nombres de solutions et le nombre total de chemins : |
Une première idée pour calculer le nombre de solutions est bien-sûr de parcourir l'arbre entièrement. On aurait par la même occasion calculé le nombre total de chemins en plus.
Mais compte tenu de ce nombre total de chemins au Solitaire anglais
On peut concevoir beaucoup d'algorithmes pour résoudre ce problème mais l'idée principale est quand même d'attribuer à chaque plateau du Solitaire le nombre de chemins qui suivant deux méthodes comptabilisent :
On peut aussi bien partir de la fin (choix 1) que du début (choix 2) :
Il y a donc un choix à faire entre connaître le nombre de chemins quelque-soit le départ pour une et une seule arrivée (choix 1) ou connaître le nombre de chemins quelque-soit l'arrivée à partir d'un et d'un seul départ (choix 2).
Le choix 2 permet donc d'avoir les deux résultats pour le même prix : une pierre, deux coups en quelque sorte.
Mais en y regardant de plus près les choix 1 et 2 sont équivalents grâce aux complémentaires.
On peut calculer le nombre de chemins entre le plateau initial et n'importe quel plateau du Solitaire et aussi le nombre de chemins entre n'importe quel plateau du Solitaire et le plateau final que ce soit avec le choix 1 ou 2 avec les complémentaires.
On peut également très bien calculer le nombre total de chemins du Solitaire (à partir du plateau initial)
avec le choix 1, c'est à dire en partant de la fin et ce encore une fois grâce aux complémentaires :
On a alors comme seules informations les nombres de chemins arrivant au plateau final mais
les chemins complémentés arrivant au plateau final
représentent alors les chemins partant du plateau initial au plateau complémenté et en additionnant
le nombre de chemins sur chaque plateau complémenté terminal, on obtient le même résultat.
A l'époque j'ai commencé par le choix 1 pour avoir les nombres
de solutions de tous les plateaux avec 32 pions (pas uniquement
celui avec le pion central enlevé au départ) qui arrivent au plateau
avec un seul pion au centre.
Le choix 1 permet de calculer le nombre de chemins de toutes les configurations
du Solitaire qui arrivent à une configuration particulière (un pion au centre par exemple).
Mais je ne savais pas encore qu'avec les complémentaires, j'aurais très bien pu
les calculer aussi avec le choix 2 qui est quand même plus logique (ou naturel).
Maintenant qu'on a l'idée générale, il faut construire un algorithme suffisamment performant, on utilisera le choix 2.
Je n'ai pas utilisé les symétries du Solitaire pour réduire le problème dans mon algorithme car il est suffisamment rapide sur mon Pentium III 450 Mhz : 10 h environ pour calculer le nombre de solutions et le nombre total de chemins du Solitaire anglais.
Néanmoins pour réduire la taille des informations enregistrés en mémoire ou sur le disque,
il peut s'avérer judicieux de supprimer les symétries (Rotation, Symétrie axiale) qui ont bien-sûr
toutes entre elles les mêmes nombres de solutions/chemins.
On ne garde alors qu'un plateau qui représente l'ensemble des symétries.
On verra aussi dans le dernier Algorithme que les complémentaires peuvent aussi réduire
le calcul du nombre total de solutions.
| Premier Algorithme : |
J'ai fait cet algorithme alors que je ne connaissais
pas encore les graphes (théorie des graphes) :
A cette époque, je ne visualisais pas vraiment le Solitaire comme maintenant : vision moins globale du graphe avec tous les différents plateaux reliés entre-eux (une partie des plateaux pour être un peu plus rigoureux).
J'avais d'ailleurs dans mon premier programme qui calculait le
nombre total de solutions, choisi de partir de la fin mais
complètement persuadé à l'époque que c'était judicieux et
même presque obligatoire pour cet algorithme :
Ce qui est évidemment faux puisque l'autre choix (choix 2) revient au même
que le choix 1 grâce aux complémentaires comme précisé ici.
Cet algorithme est basé sur une Fonction d'adressage bijective notée F qui transforme un Solitaire à n bits en son numéro dans sa classe d'équivalence binaire et inversement (avec F-1).
C'est la clef de l'algorithme qui m'a permis d'ailleurs de découvrir une formule mathématique que je ne connaissais pas auparavant pour calculer F rapidement.
On utilise alors une table Tn (31>n>1) utilisant si possible toute la mémoire physique disponible avec comme valeurs les nombres de chemins allant du Solitaire de départ vers le plateau P à n pions avec F(P) comme index de la table.
Le problème est alors que la mémoire physique disponible est insuffisante sur les ordinateurs actuels :
(5-10 Gigaoctets seraient nécessaires) :
En effet, il y a
Pour garder l'avantage de la mémoire physique par rapport au disque, on est obligé de fenêtrer la Table Tn, c'est à dire de découper la table en autant de bloc correspondant à la mémoire physique disponible de même taille.
Ce découpage a une contrepartie : il faut faire autant de traitements identiques qu'il y a de blocs ou presque, ce qui multiplie le temps de l'algorithme par le nombre de blocs. Évidemment, plus la mémoire physique disponible est importante, plus l'algorithme s'effectuera rapidement presque linéairement (proportionnellement).
Pour optimiser un peu, on crée une table binaire des solitaires déjà traités pour éviter de
faire plusieurs fois le même calcul. En fait cette table indique si un plateau du Solitaire
a déjà été traité complètement : c'est à dire si il n'a pas de successeur par exemple
ou si tous ses successeurs ont déjà été traité, ce qu'on peut savoir si ils appartiennent
à des fenêtres inférieures ou égales à la fenêtre actuelle.
La taille de cette table est au maximum de
Pour calculer le nombre total de chemins, il suffit d'additionner les nombre de chemins à chaque plateau terminal.
L'algorithme se présente alors sous cette forme :
On a alors les 32 fichiers Plateaux32,...,Plateaux1
avec tous les nombres de chemins associés aux plateaux à n pions.
Et on a aussi la variable globale nombre de chemins total.
| Deuxième Algorithme : |
Le premier algorithme est un peu compliqué même si très performant. C'est pourquoi je vous propose cet autre algorithme peut-être même plus rapide si bien optimisé :
On utilisera une structure de donnée classique : Un arbre dit équilibré ou plus précisément un arbre AVL du nom de ces inventeurs (Adelson-Velskii et Landis).
Un arbre AVL si vous ne connaissez pas est un arbre binaire
de recherche équilibré (équilibré en hauteur).
On peut aussi utiliser un
Cet arbre nous permet d'accéder, détruire ou ajouter un élément en Log2(n). (Complexité d'ordre logarithmique)
Un nœud de l'arbre (une feuille) représente un plateau
de Solitaire à n pions codés sur 33 bits avec le nombre de chemins menant jusqu'à lui
(choix 2).
On ajoutera aussi le nombre de ces prédécesseurs (plateaux parents)
qu'on calculera à la création du nœud, tout ça dans le but d'optimiser un peu (en fait beaucoup).
D'ailleurs, sur l'ensemble des plateaux du Solitaire, le plateau qui possède le plus de prédécesseurs
a pour complémentaire le plateau qui possède le plus de successeurs.
Le nombre maximum de prédécesseurs est donc aussi le nombre maximum de successeurs.
Dans cet algorithme, l'arbre AVL remplira vite la mémoire physique
avec les plateaux de 10 à 20 pions notamment :
On enregistrera alors sur disque tous les plateaux qui n'ont pu être traité
directement dans la mémoire physique, en attendant la fin de traitement
des plateaux dans la mémoire.
On risque donc de se retrouver avec un fichier plateauxn en attente quasiment aussi volumineux que plateauxn, plus de 50% de la taille du fichier plateauxn aux stades extrêmes (tout dépend de la mémoire vive).
Cela évite le fenêtrage du premier algorithme mais il n'est pas pour autant plus rapide que le premier algorithme sauf s'il est vraiment bien optimisé je pense.
Il nécessite en tout cas comme pour le premier algorithme un espace disque assez conséquent mais ça ne pose pas de problème avec les disques actuels de plusieurs Giga-octets (dizaines mêmes).
Je ne l'ai jamais essayé donc à vous de me dire s'il est efficace. En tout cas, la mémoire vive disponible est déterminante pour sa vitesse tout comme avec le premier algorithme.
| Un dernier Algorithme : |
Cet algorithme utilise les propriétés des Solitaires complémentaires vues plus haut.
Il permet de calculer le nombre total de solutions plus rapidement mais pas le nombre total de chemins.
Il nécessite d'utiliser un des deux algorithmes précédents pour déjà calculer les nombres de chemins menant à l'ensemble des plateaux à 17 pions : Fichier Plateaux17.
A partir de ce seul fichier, on est capable de calculer d'un coup le nombre total de solutions du Solitaire anglais, ce qui permet d'atteindre ce résultat beaucoup plus vite : près de deux fois plus vite puisque plus de la moitié des calculs restaient à faire à ce stade (moitié des algorithmes précédents).
L'algorithme ne prend pas plus de temps que les étapes des algorithmes précédents qui permettent de passer des plateaux à 17 pions aux plateaux à 16 pions, d'où le temps gagné.
Le nombre total de solutions au Solitaire anglais peut être calculé avec cette formule :

La formule exploite les propriétés des complémentaires :
Elle additionne n fois les nombres de solutions
qui passent par les plateaux Plateaux17(i) :
En effet on connaît le nombre de chemins allant du plateau initial aux plateaux à 17 pions (Fichier plateaux17).
Grâce aux complémentaires, on connaît alors aussi le nombre de chemins allant des plateaux à 16 pions au plateau final.
Il suffit donc de multiplier le nombre de chemins menant à un plateau à 17 pions par le nombre de chemins de tous ses successeurs qui mènent à la solution (donc par la somme de la variable nombre de chemins de tous ses successeurs).
On pourra adapter le premier algorithme pour faire ce calcul rapidement mais d'autres méthodes sont possibles évidemment.
Algorithme (adaptation du premier algorithme) :
Il faut un algorithme capable de lire rapidement les nombres de chemins des successeurs complémentés d'un plateau à 17 pions (successeurs complémentés à 17 pions aussi).
En fait, il suffit simplement de remplacer la fenêtre d'écriture du premier algorithme par une fenêtre en lecture avec tous les nombres de chemins des plateaux à 17 pions.
Vous voyez, c'est quasiment le même algorithme que le premier à part qu'on l'a adapté au calcul de cette formule.
La vitesse de l'algorithme dépendra donc linéairement
de la mémoire physique utilisée et allouée comme pour
le premier algorithme :
Vitesse proportionnelle au nombre de fenêtres nécessaires à représenter l'ensemble
des nombres de chemins des plateaux à 17 pions
| Conclusion : |
Voilà pour terminer, je vous conseille le programme
de Philippe Basciano qui résout toutes sortes de configurations
et de Solitaires (anglais, français,...).
Télécharger cet excellent programme :
PEG SOLITAIRE 1.99 (Philippe Basciano)
Je vous conseille aussi le programme de Mark Williams
qui vous aidera à gagner au Solitaire anglais en affichant
les coups gagnants (winning moves comme disent les
anglo-saxons).
Télécharger cet autre excellent programme :
PegSol 1.1 (Mark Williams)
Sinon, vos remarques sont les bienvenues à : eternitygames@free.fr

Avec tout ça, vous serez imbattable au Solitaire...


