L'analyse de ce système sous Mapple : solitaire position reduite.zip

Rappel d'algèbre linéaire :

Déterminons le rang de cette matrice en calculant un déterminant non nul d'ordre le plus élevé parmi l'ensemble des matrices carrées issues de cette matrice 9x20.

Prenons par exemple le déterminant suivant issues des colonnes représentées par les inconnues : x1,x2,x3,x4,x5,x6,x7,x8,a0 :

Ce déterminant d'ordre 9 étant non nul, le rang r de la matrice est de 9.

Suivant le théorème de Fontené-Rouché, on a r=9 équations principales avec r=9 inconnues principales : x1,x2,x3,x4,x5,x6,x7,x8,a0 et le rang étant égal au nombre d'équations du système, nous avons 20-9 = 11 inconnues non principales ou paramètres : x9,x10,x11,x12,a1,b0,b1,a'0,a'1,b'0,b'1 et le système s'écrit matriciellement :

Méthode 1 :

On a :

M1 X=C

Det(M1)= -16  (comme on l'a vu plus haut)

Det(M1) étant différent de 0, M1 est une matrice régulière et possède une matrice inverse :

On pose :

Rappel du calcul de l'inverse d'un matrice carrée (par élimination de Gauss) :

Remarque : en faisant le produit des éléments sur la diagonale de la matrice, on  un déterminant égal à (-1)(-2)(1)(-2)(1)(-2)(1)(-2)(-1) = 16 (il n'est pas égal au déterminant de la matrice d'origine qui était de -16 car nous avons fait 3 permutations de lignes lors du calcul, ce qui change le signe du déterminant).

On a donc bien :

Rappel de calcul matriciel :

Revenons à :

Donc :

Méthode 2 (que je préfère car c'est que du calcul matriciel donc facilement numérisable) :

On avait :

On a :

Donc :

Calcul matriciel :

Et on retrouve :

La solution générale de ce système est donc de la forme (avec les 11 paramètres x9,x10,x11,x12,a1,b0,b1,a'0,a'1,b'0,b'1) :

Comme précédemment vu ici, on a en particulier :

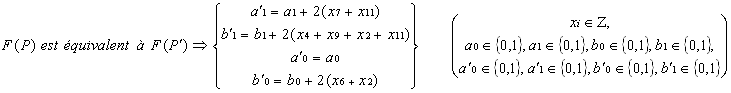
Donc a1 et a'1 ont la même parité, b1 et b'1 ont la même parité, a0 et a'0 sont égaux et b0 et b'0 ont la même parité.

L'unicité est ainsi démontrée.

visiteurs depuis le 15 février 2001